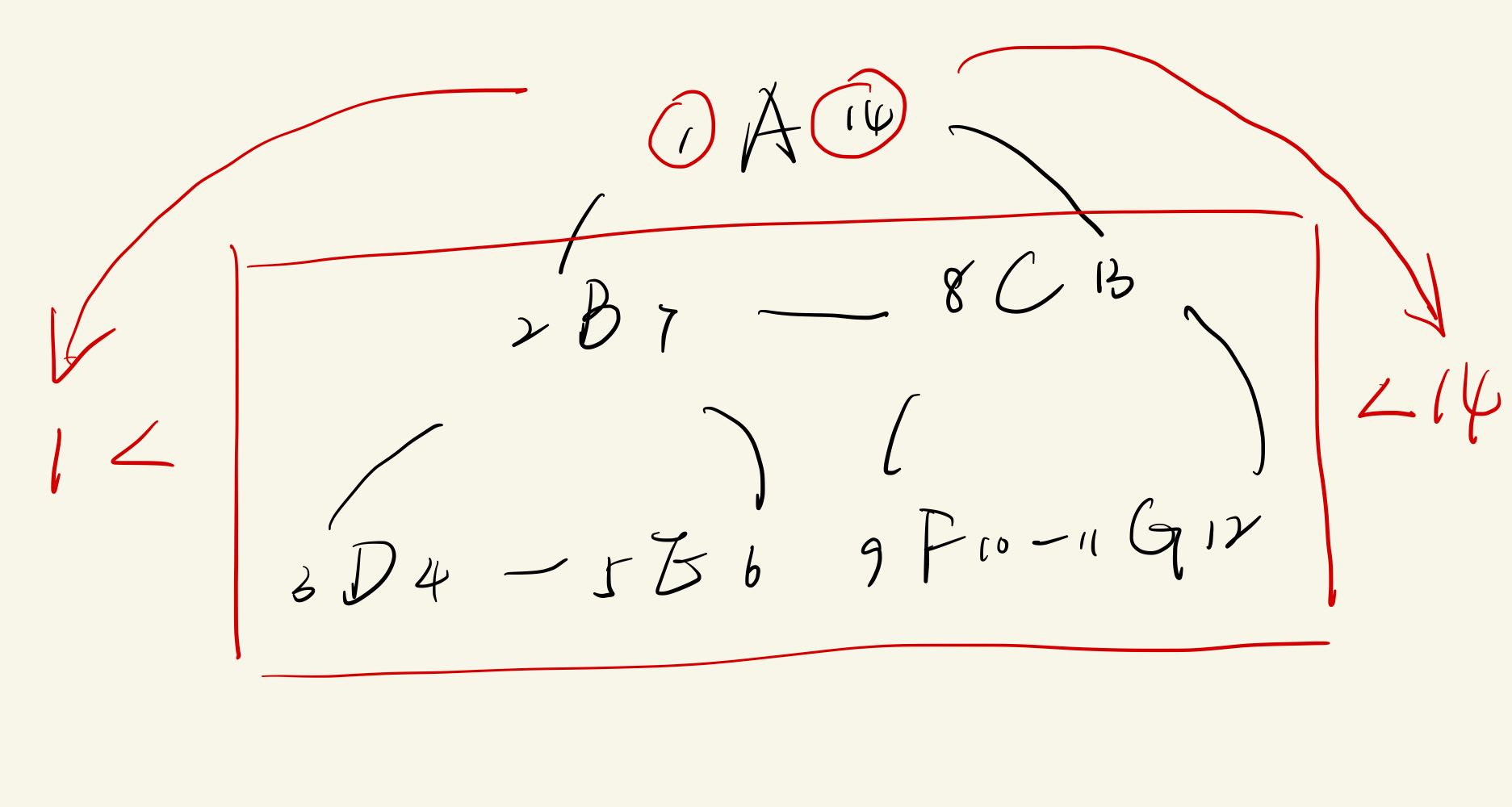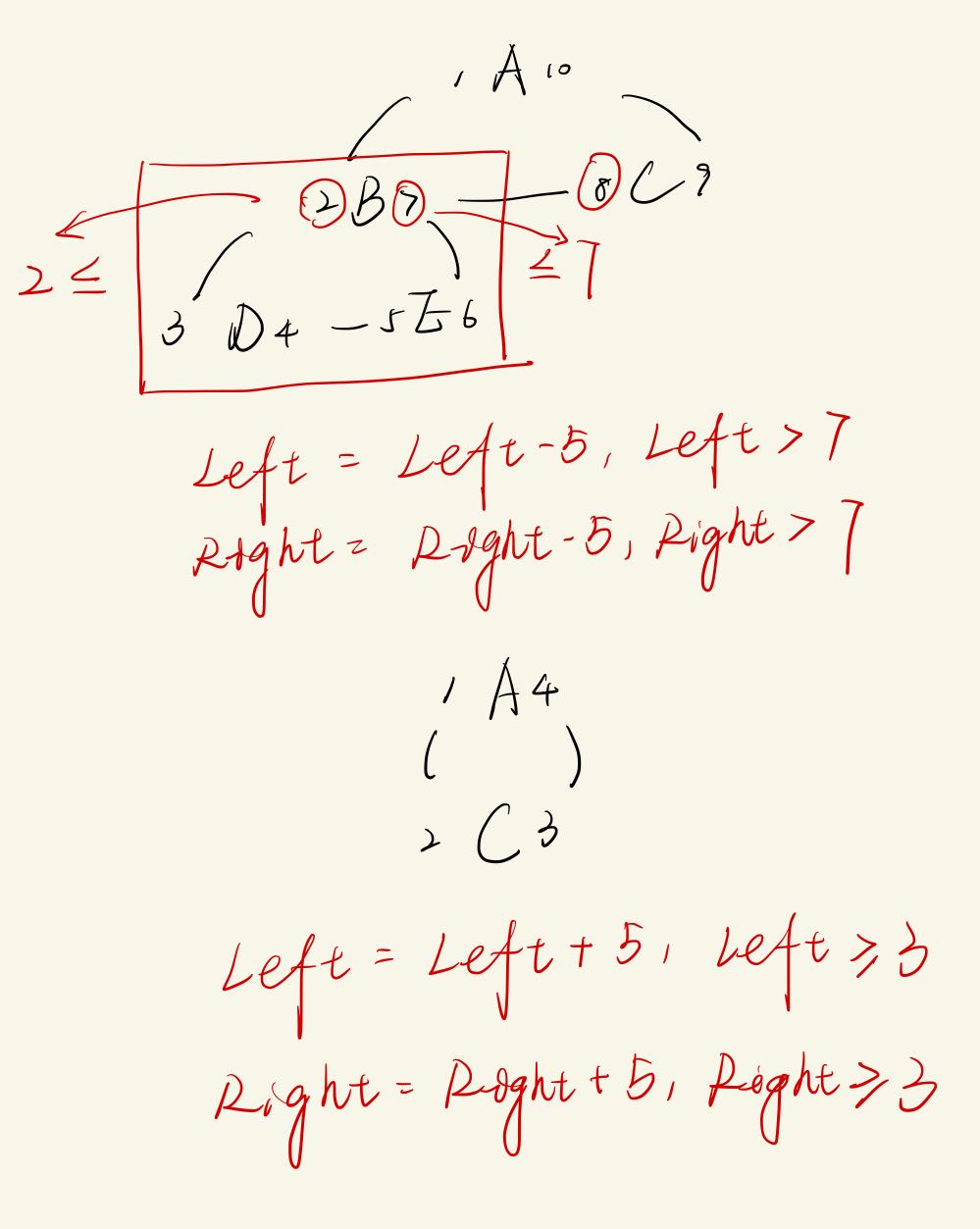如何在数据库中存储层次结构
常见场景
- 公司:公司 - 部门 - 子部门
- 人员:领导 - 员工
- 文件:根目录 - 文件夹 - 文件
- 关系:group - child
实例
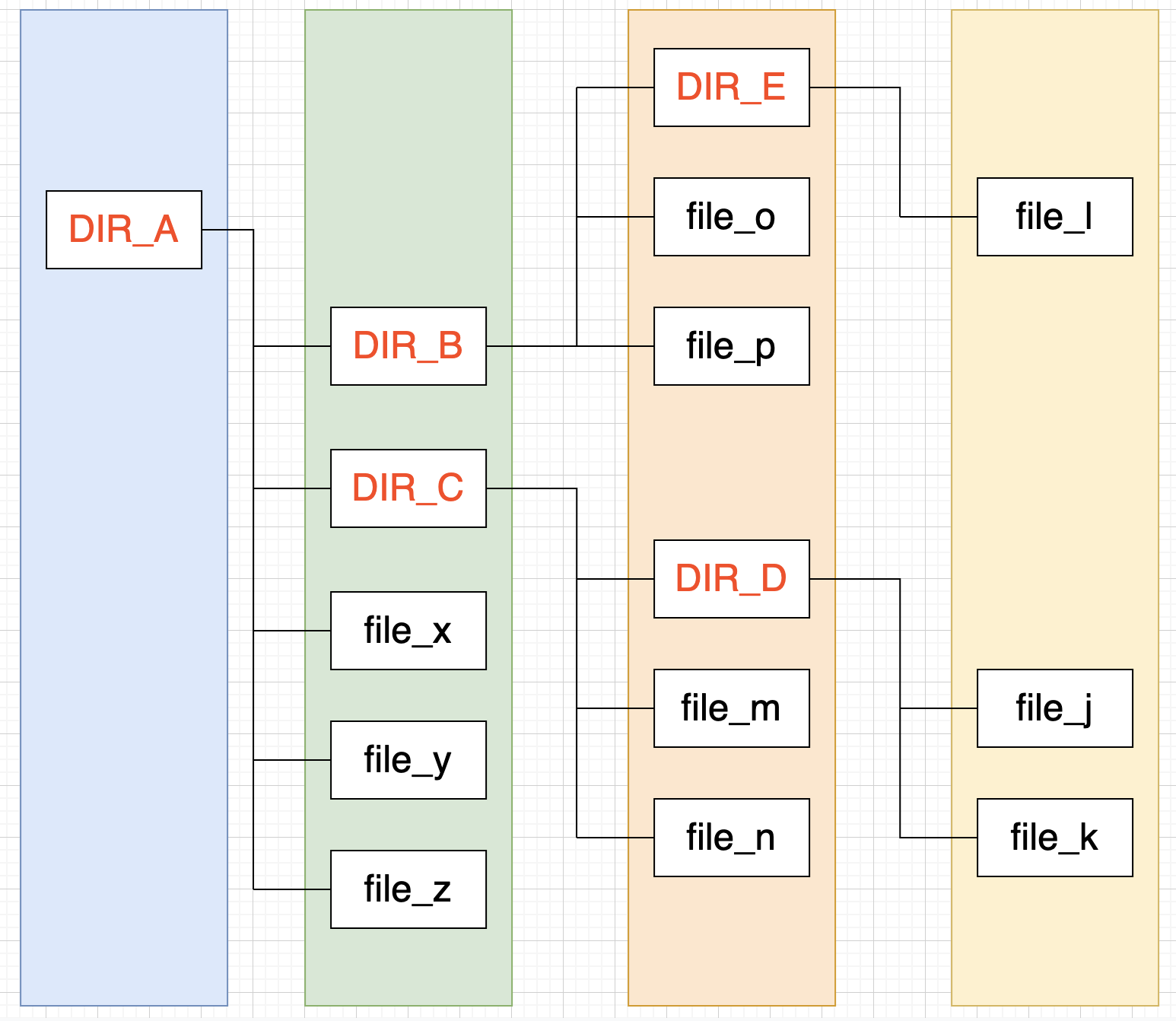
转成树型
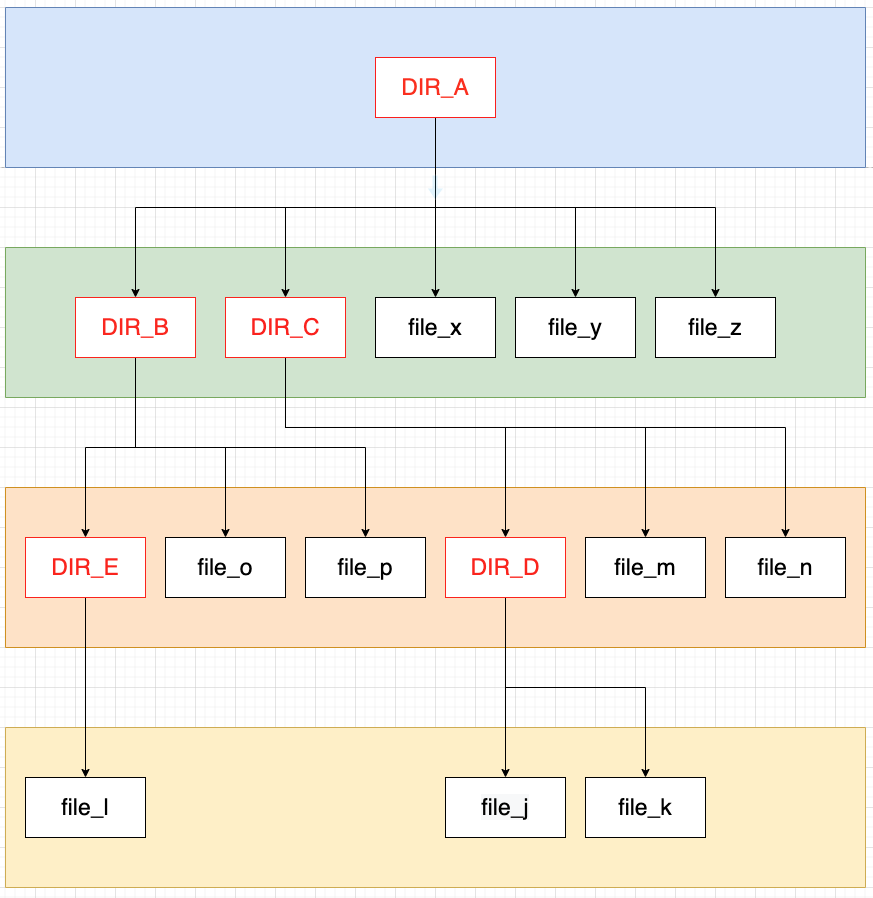
回头看
之前提到的几种方案(Adjacency_List, Path_Enumerations, Closure_Table)都能够一定程度地满足需求,但是各自具有不可避免的弊端。
Adjacency_List: 层级查询 -> ∞
Path_Enumerations: 深度限制
Closure_Table: 空间消耗大,层级删改 -> ∞
Nested Sets
根据树的深度遍历对节点编号,记录首、末次访问到该节点的数字。通过比较数字或的层级结构关系。
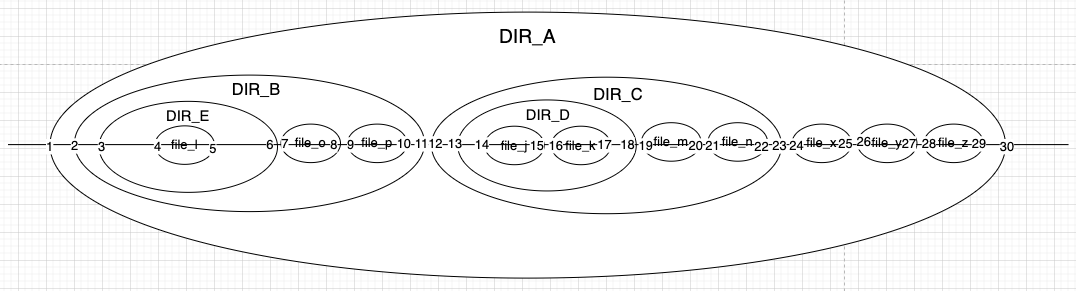
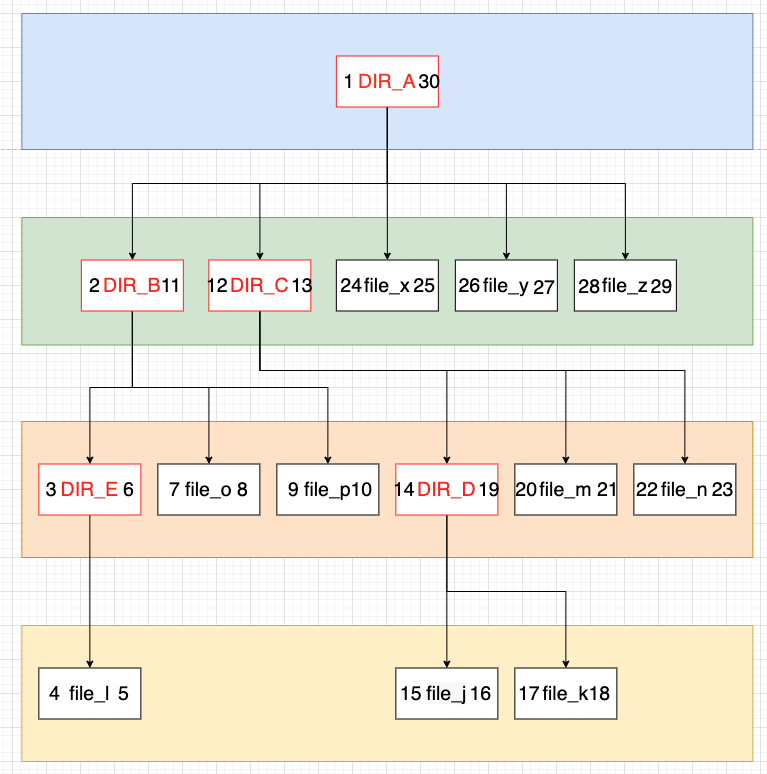
| id | name | left | right |
|---|
| 1 | DIR_A | 1 | 30 |
| 2 | DIR_B | 2 | 11 |
| 3 | DIR_C | 12 | 13 |
| 4 | file_x | 24 | 25 |
| 5 | file_y | 26 | 27 |
| 6 | file_z | 28 | 29 |
| 7 | DIR_E | 3 | 6 |
| 8 | file_o | 7 | 8 |
| 9 | file_p | 9 | 10 |
| 10 | DIR_D | 14 | 19 |
| 11 | file_m | 20 | 21 |
| 12 | file_n | 22 | 23 |
| 13 | file_l | 4 | 5 |
| 14 | file_j | 15 | 16 |
| 15 | file_k | 17 | 18 |
各种情况的处理代价
增
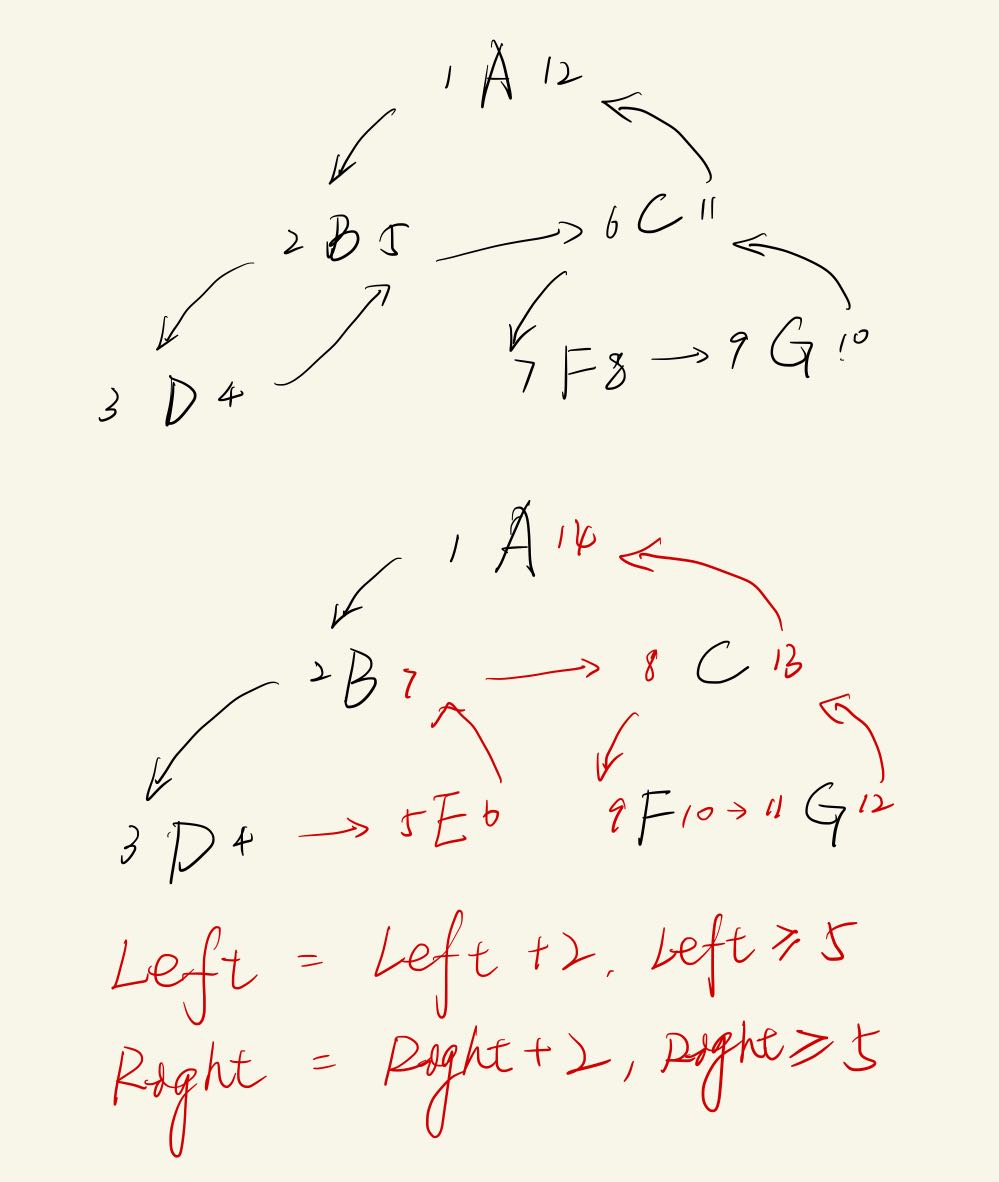
代价:-> O(n),更新会影响到其他子树
输入:name. parent_id
执行:
1
2
3
4
5
6
| parent = $(select * from table where id = $id);
insert into table(name, left, right) values($name, $parent.right, $parent.right + 1);
update table set left = left + 2 where left >= $parent.right;
update table set right = right + 2 where right >= $parent.right;
|
删
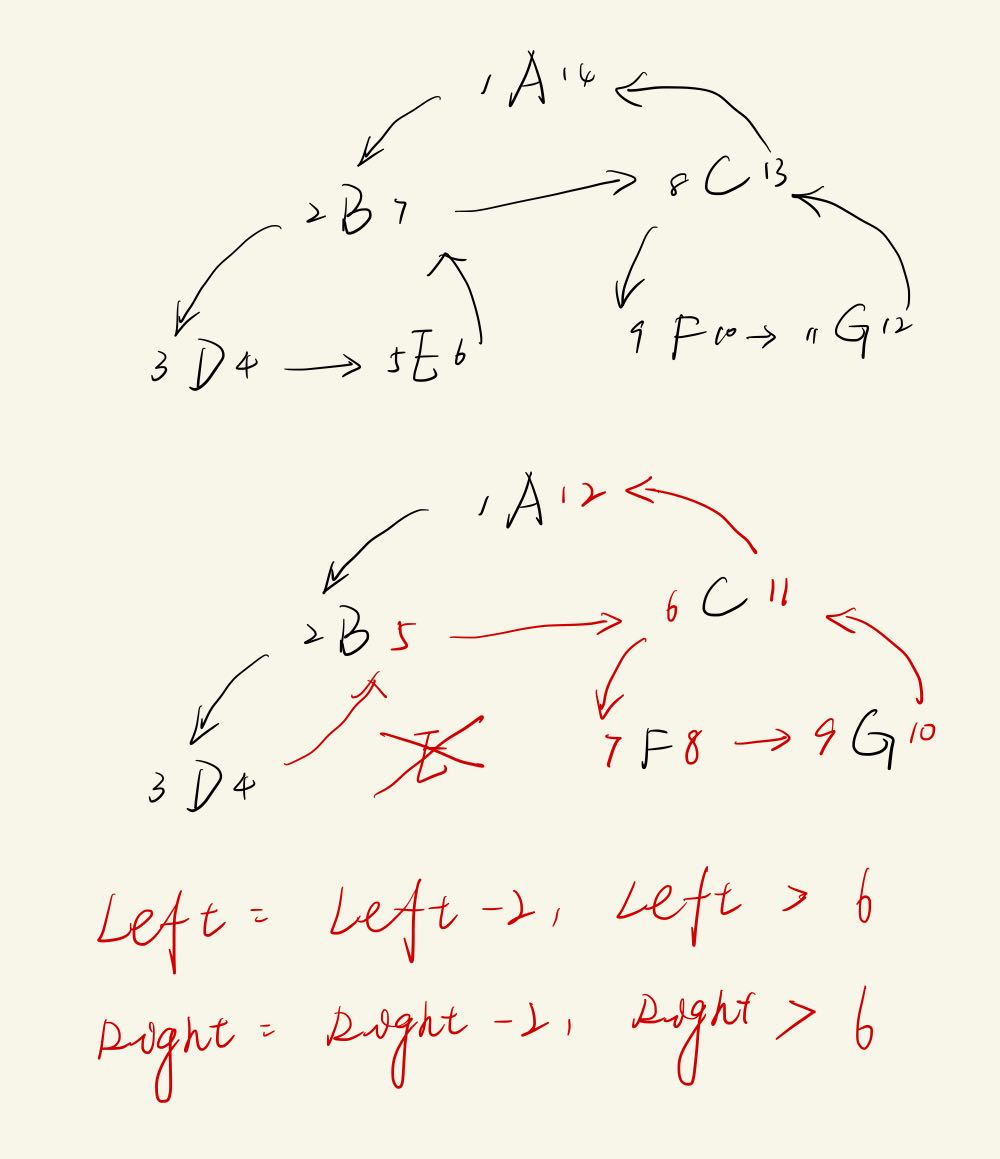
代价:-> O(n),先删除节点以及子树,并对其他子树进行修改
输入:id
执行:
1
2
3
4
5
6
7
| current = $(select * from table where id = $id);
delete from table where left >= $current.left and right <= $current.right;
d = current.right - current.right + 1;
update table set left = left - $d where left > $current.right;
update table set right = right - $d where right > $current.right;
|
改
代价:-> O(1)
id, other info
执行:
1
| update table set info where id = $id;
|
查
查自己
代价:-> O(1)
输入:id
执行:
1
| select * from table where id = $id
|
查下一级
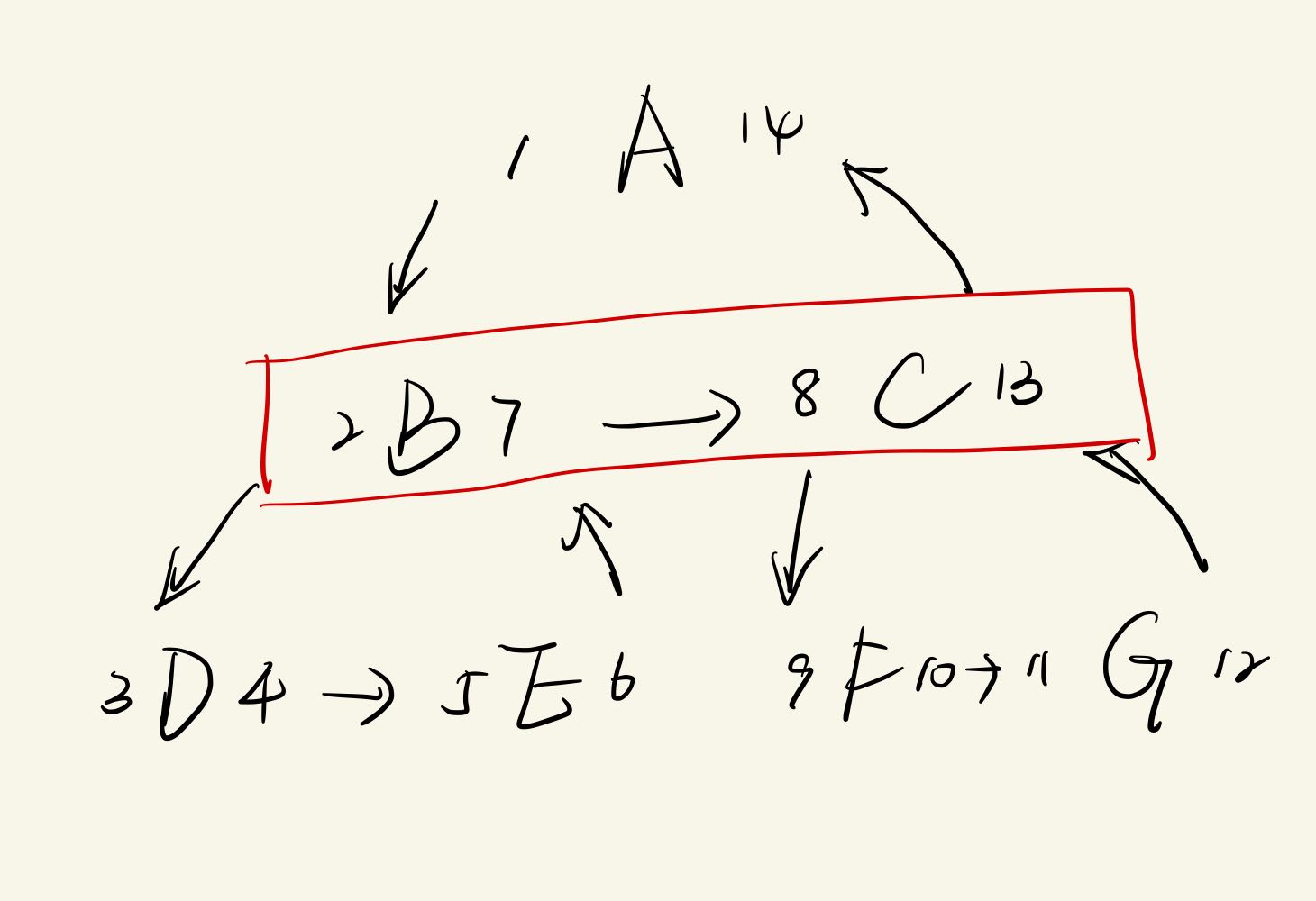
代价:-> O(n)
输入:id
执行:
1
2
3
4
5
6
7
| select distinct Child.Node, Child.Left, Child.Right
from table as child, table as parent
where parent.left < child.left and parent.right > child.right -- associate Child Nodes with ancestors
group by child.node, child.left, child.right
having max(parent.left) = $parent.left -- Subset for those with the given Parent Node as the nearest ancestor
这类查询可以通过增加一列来简化。例如,增加depth列记录当前节点深度,或者parent_id列记录父节点(和Adjacency List混用),但增加了维护成本
|
查所有子集
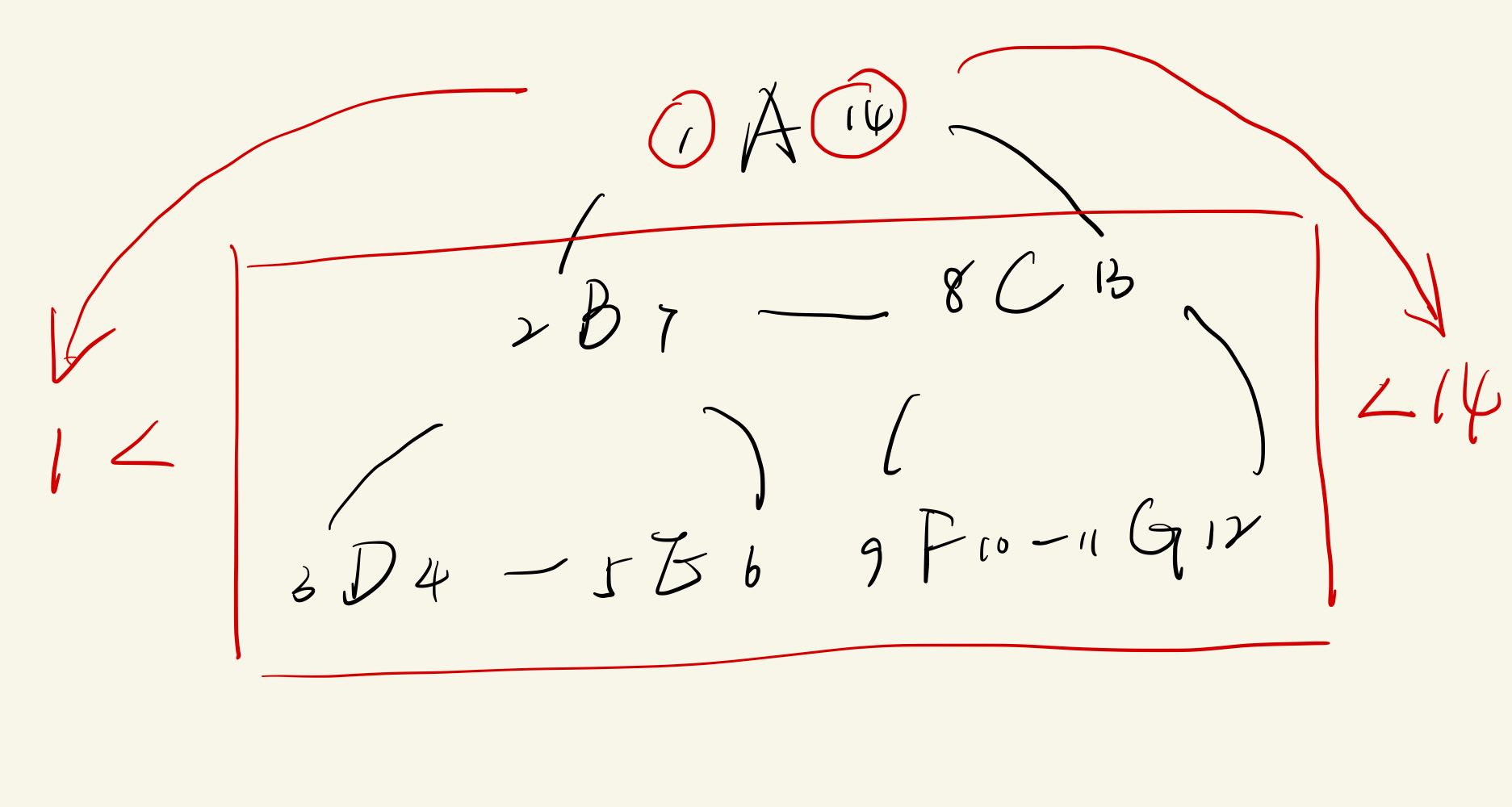
代价:-> O(n)
输入:path
执行:
1
2
3
4
5
| select *
from table
where left > $parent.left
and right < $parent.right
order by left asc;
|
移动
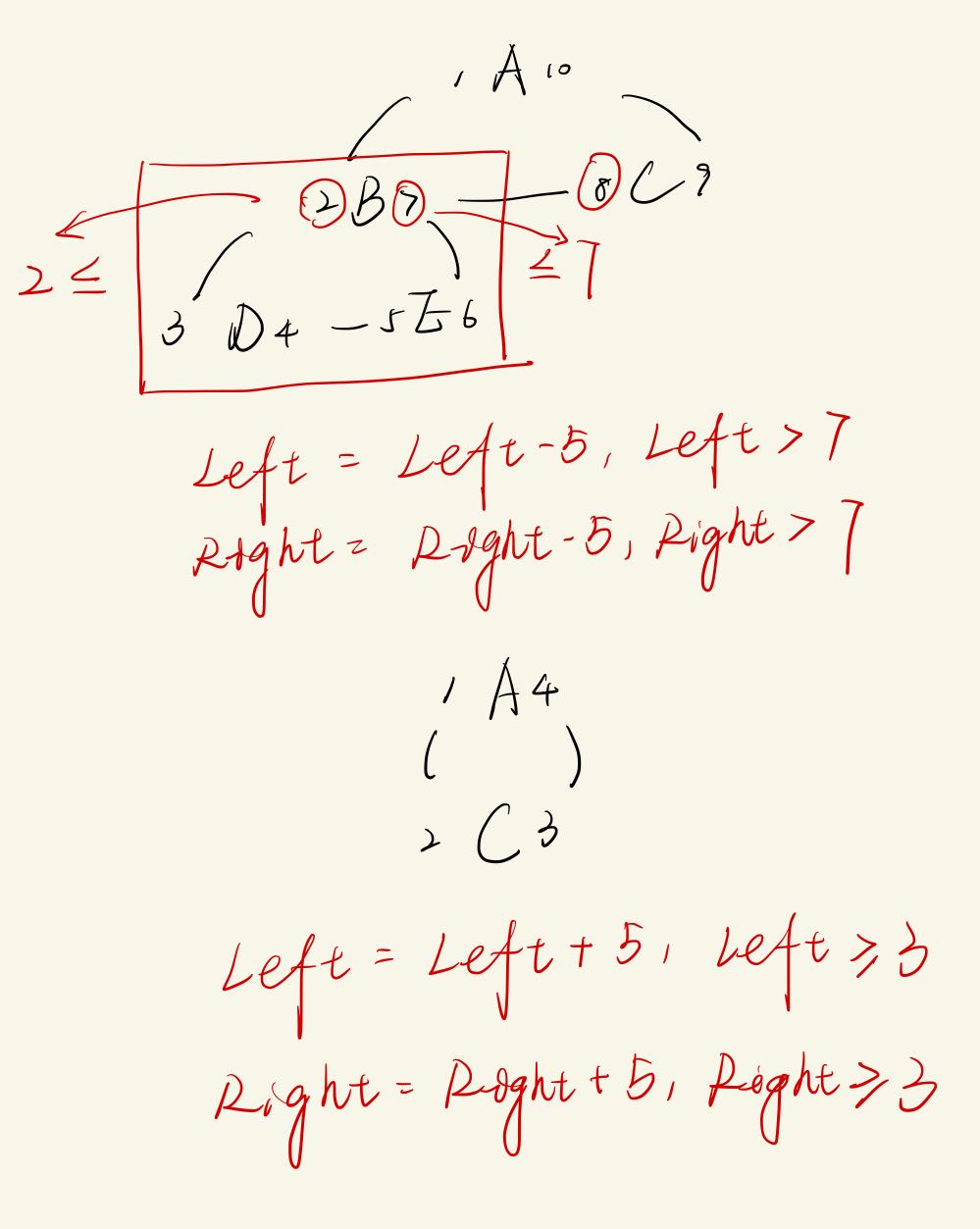
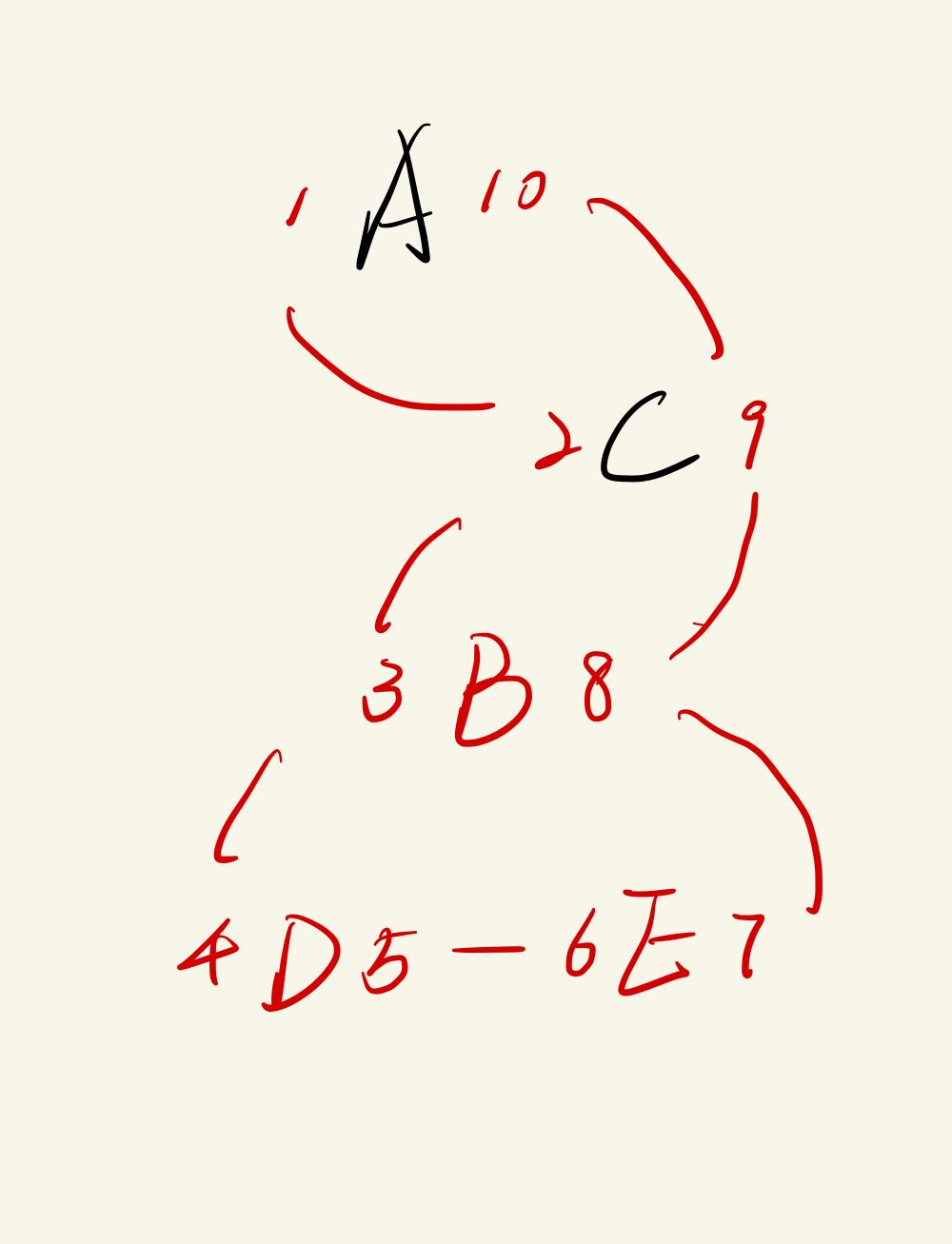
代价:-> O(n)
输入:id, new_parent_id
执行:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
## 先执行 DEL,再执行 ADD
current = $(
select *
from table
where id = $id
);
## 查询父节点
old_parent = $(
select * from table
where left < $current.left
and right > $current.right
order by left desc
limit 1
);
-- 查询移动节点以及子节点的总数
node_count = $(
select count(*)
from table
where left >= $current.left
and right <= $current.right
);
update table
set left = left - node_count*2,
where left > $current.right;
update table
set right = right - node_count*2
where right > $current.right;
## 更新子节点
update table
set left = left + ($new_parent.right - $current.left),
right = right + ($new_parent.right - $current.left)
where left >= $current.left
and right <= $current.right
$current.left = $new_parent.right;
$current.right = $new_parent.right + 1;
update table
set left = left + node_count*2,
where left > $current.right;
update table
set right = right + node_count*2
where right > $current.right;
|
总结
可以和邻接表同时使用
优点 : 消除递归操作,实现无限分组
缺点 : 增 删 改影响范围大
适用 : 强要求无限层级深度
比较
| T | 增 | 删 | 改 | 查自己 | 查下一级 | 查所有子集 | 移动 | 适用 |
|---|
| Adjacency List | O(1) | ∞ | O(1) | O(1) | O(n) | O(n) | O(1) | 不涉及“所有子集”操作,严格按照层级一层层地查询 |
| Closure Table | O(n) | O(n) | O(1) | O(1) | O(n) | O(n) | O(n) | 有固定的层级深度,并且层级不多 |
| Path | O(1) | O(n) | O(n) | O(1) | O(n) | O(n) | O(n) | 对层级深度有一定限制,并且需求对所有子集进行操作 |
| Netsted Sets | O(n) | O(n) | O(1) | O(1) | O(n) | O(n) | O(n) | 强要求无限层级深度 |