Storing Hierarchical data by 【Adjacency List】

如何在数据库中存储层次结构

常见场景

公司：公司 - 部门 - 子部门
人员：领导 - 员工
文件：根目录 - 文件夹 - 文件
关系：group - child

实例

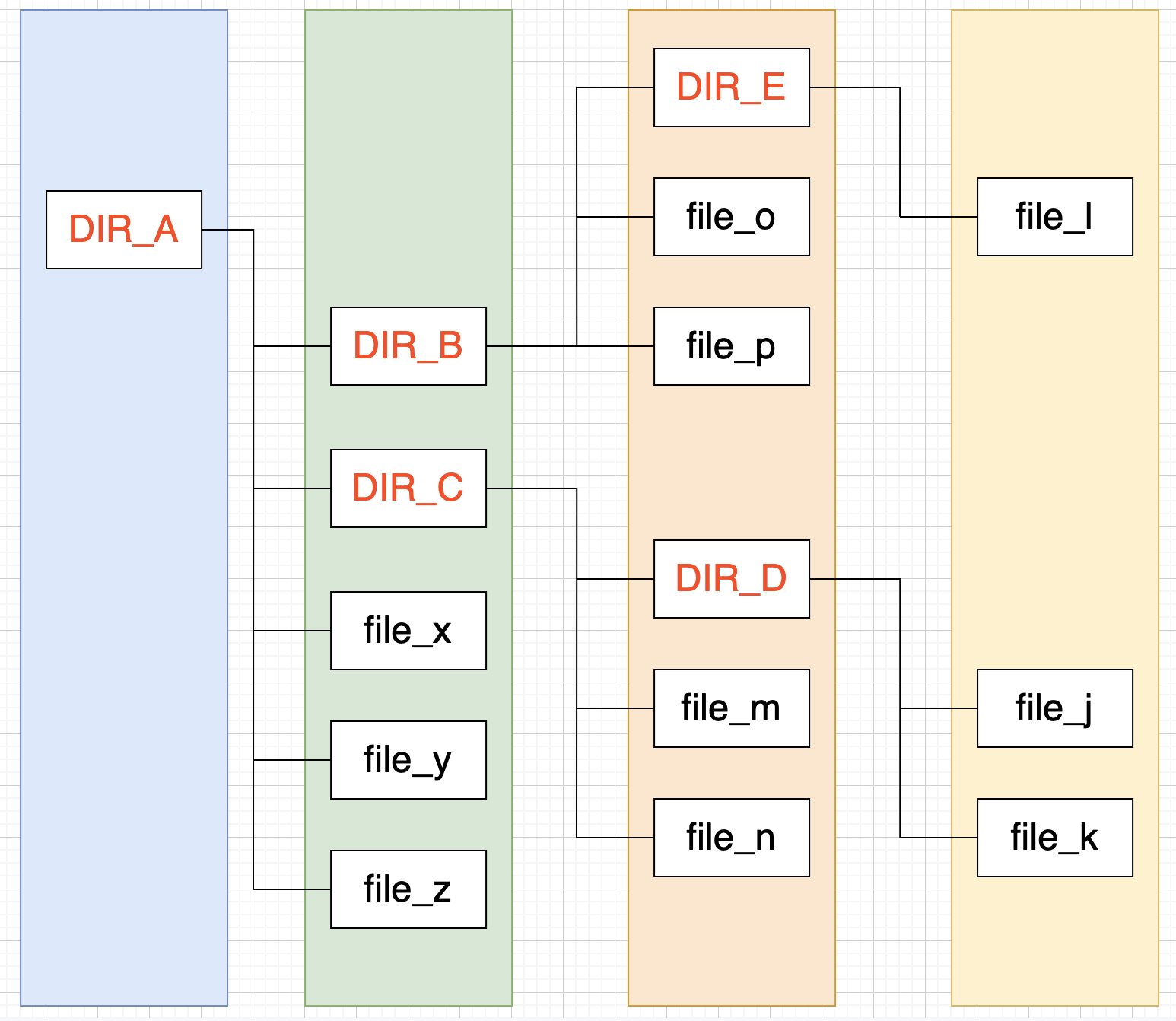
转成树型

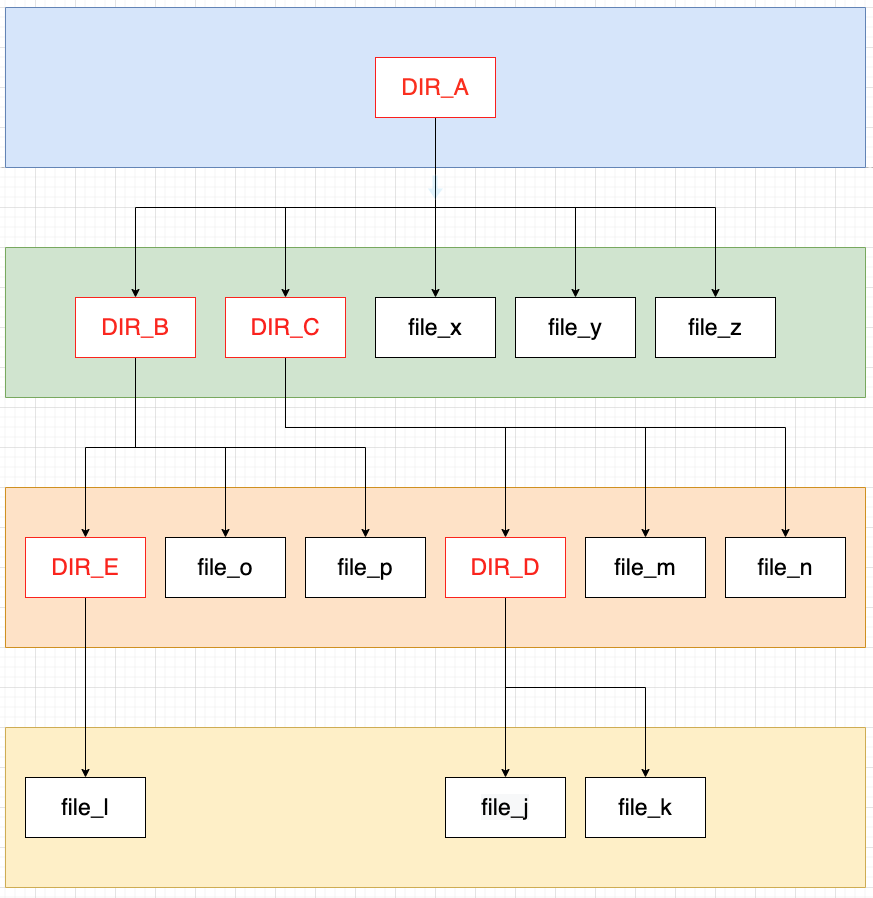
Adjacency List 邻接表

存储当前节点的父节点信息（parent_id），通过 parent_id 相关联

id	name	parent_id
1	DIR_A	root
2	DIR_B	1
3	DIR_C	1
4	file_x	1
5	file_y	1
6	file_z	1
7	DIR_E	2
8	file_o	2
9	file_p	2
10	DIR_D	3
11	file_m	3
12	file_n	3
13	file_l	7
14	file_j	10
15	file_k	10

各种情况的处理代价

1
2
3
O(1)：有限的操作次数，有限的影响范围
O(n)：有限的操作次数，无限的影响范围
∞：无限的操作次数

增

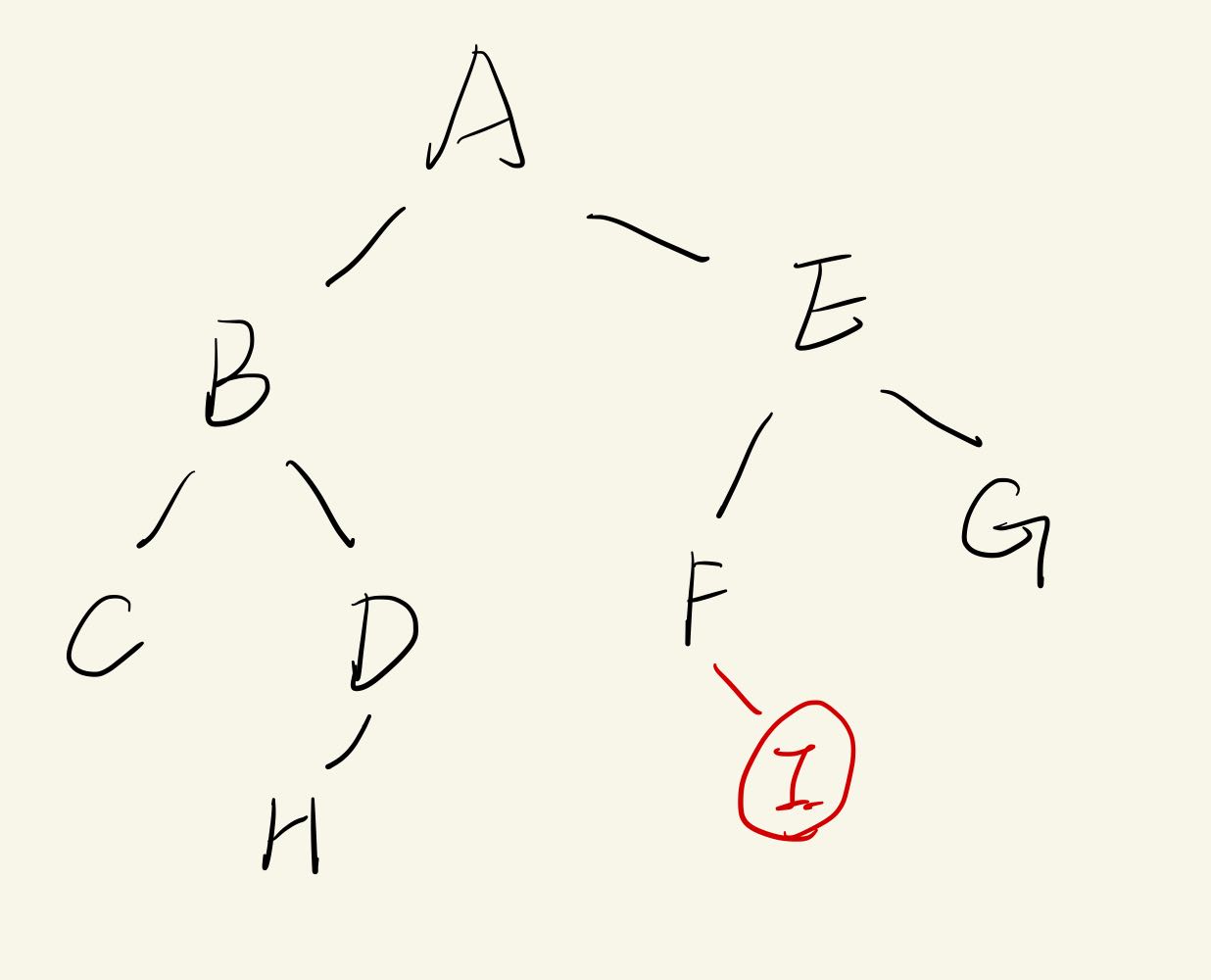
代价：-> O(1)
输入：name, parent_id
执行：

1
insert into table(name, parent_id) values($name, $parent_id);

id	name	parent_id
13	file_l	7
14	file_j	10
15	file_k	10
16(add)	file_ADD	1

删

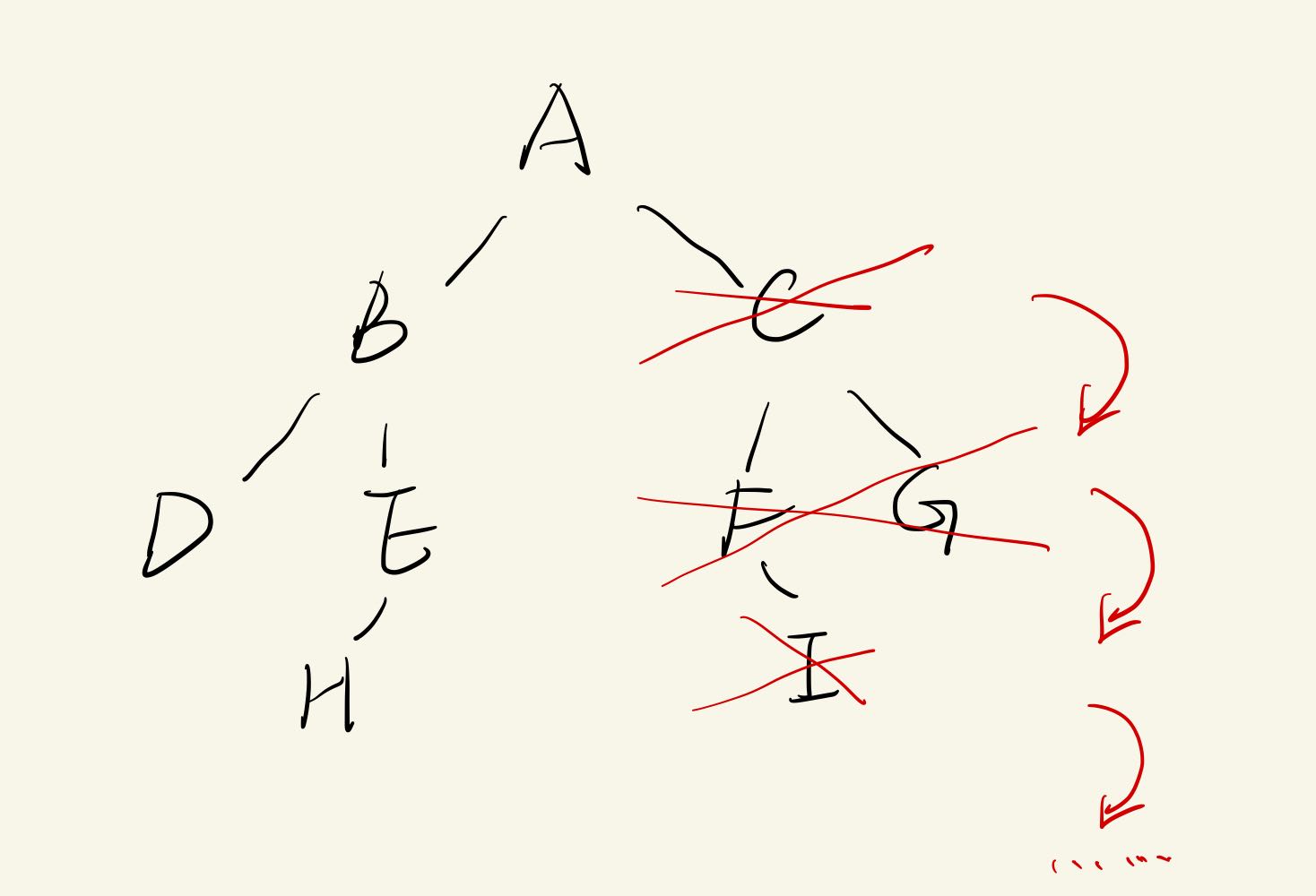
需要递归删除

代价：-> ∞
输入：id
递归执行：

1
2
3
4
5
ids[] = $id
while (ids is not empty) {
    delete from table where id in $ids;
    ids = $(select id from table where parent_id in $ids);
}

当然也可以只删除直接下级，但会留下“悬浮节点”

改

代价：-> O(1)
输入：id, other info
执行：

1
update table set info where id = $id

查

查自己

代价：-> O(1)
输入：id
执行：

1
select * from table where id = $id

查下一级

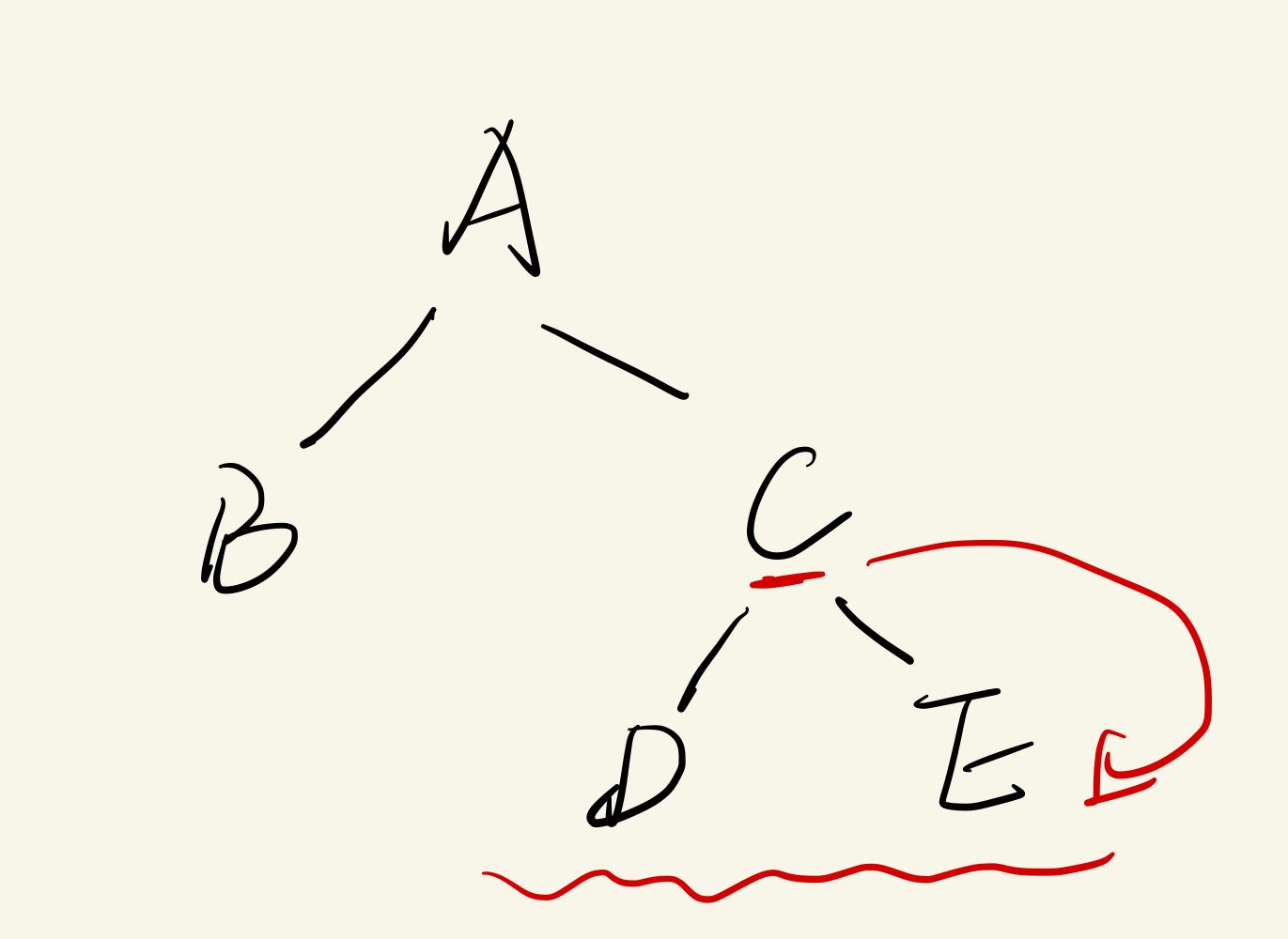
代价：-> O(n)
输入：id
执行：

1
select * from table where parent_id = $id

查所有子集

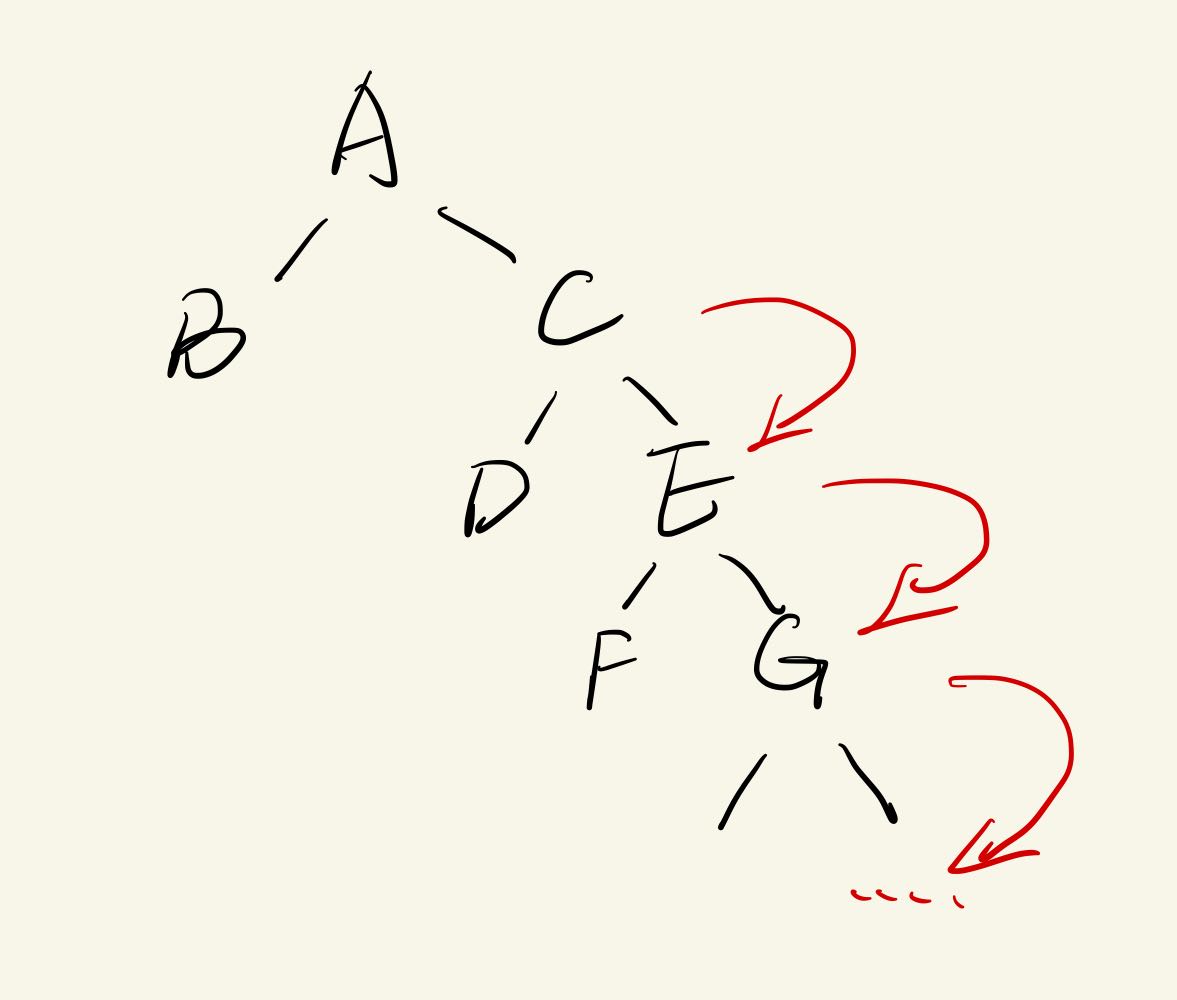
代价：-> ∞
输入：id
执行：

1
2
3
4
5
6
ids[] = $id
sub_ids[] = $id
while (sub_ids is not empty) {
    sub_ids = $(select id from table where id in sub_ids);
    ids += sub_ids;
}

移动

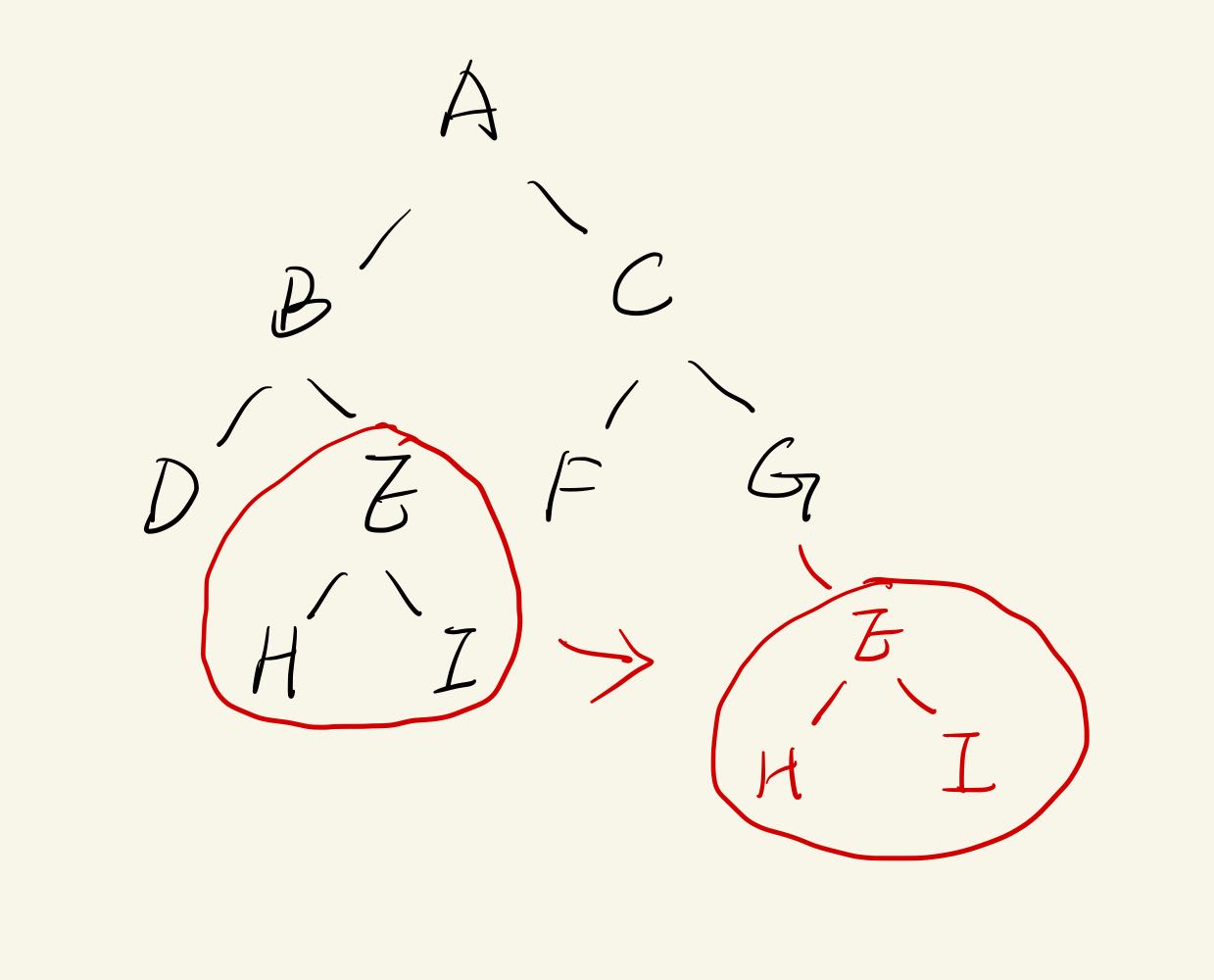
代价：-> O(1)
输入：id, new_parent_id
执行：

1
update table set parent_id = $new_parent_id where id = $id;

总结

优点 : 进行增加、修改、移动时代价很低; 查询自己、直接下级非常方便
缺点 : 如若需要使用层级结构，例如获取所有子目录，所有下级，代价趋近∞（致命）
适用 : 不涉及“所有子集”，严格按照层级一层层地查询