R[week2] Segmentation Code

R: 4.3.2 (2023-10-31)
R studio: 2023.12.1+402 (2023.12.1+402)

Segmentation data

• 年龄（age）
• 性别（gender）
• 收入（income）
• 孩子数量（kids）
• 是否拥有或租赁住房（ownHome）
• 当前是否订阅所提供的会员服务（subscribe）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
> seg.df <- read.csv("Data_Segmentation.csv", stringsAsFactors = TRUE)

> head(seg.df, n=8)

> head(seg.df, n=8)
       age gender   income kids ownHome subscribe
1 47.31613   Male 49482.81    2   ownNo     subNo
2 31.38684   Male 35546.29    1  ownYes     subNo
3 43.20034   Male 44169.19    0  ownYes     subNo
4 37.31700 Female 81041.99    1   ownNo     subNo
5 40.95439 Female 79353.01    3  ownYes     subNo
6 43.03387   Male 58143.36    4  ownYes     subNo
7 37.55696   Male 19282.23    3   ownNo     subNo
8 28.45129   Male 47245.24    0   ownNo     subNo

Recode factor into numeric data

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
> seg.df$gender <- ifelse(seg.df$gender=="Male",0,1) 
> seg.df$ownHome <- ifelse(seg.df$ownHome == "ownNo", 0,1) 
> seg.df$subscribe <- ifelse(seg.df$subscribe == "subNo", 0,1)
> head(seg.df)

       age gender   income kids ownHome subscribe
1 47.31613      0 49482.81    2       0         0
2 31.38684      0 35546.29    1       1         0
3 43.20034      0 44169.19    0       1         0
4 37.31700      1 81041.99    1       0         0
5 40.95439      1 79353.01    3       1         0
6 43.03387      0 58143.36    4       1         0

Rescaling the data

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
> seg.df.sc <- seg.df

> seg.df.sc[, c(1,3,4)] <- scale(seg.df[, c(1,3,4)])

## We only need to standardize continuous variables.
> head(seg.df.sc)
          age gender     income       kids ownHome subscribe
1  0.48133138      0 -0.0721898  0.5183027       0         0
2 -0.77221071      0 -0.7642562 -0.1917010       1         0
3  0.15744276      0 -0.3360563 -0.9017048       1         0
4 -0.30554218      1  1.4949908 -0.1917010       0         0
5 -0.01930052      1  1.4111190  1.2283065       1         0
6  0.14434200      0  0.3578800  1.9383103       1         0

> summary(seg.df.sc, digits = 2)
      age            gender         income            kids          ownHome       subscribe   
 Min.   :-1.73   Min.   :0.00   Min.   :-2.787   Min.   :-0.90   Min.   :0.00   Min.   :0.00  
 1st Qu.:-0.64   1st Qu.:0.00   1st Qu.:-0.560   1st Qu.:-0.90   1st Qu.:0.00   1st Qu.:0.00  
 Median :-0.13   Median :1.00   Median : 0.054   Median :-0.19   Median :0.00   Median :0.00  
 Mean   : 0.00   Mean   :0.52   Mean   : 0.000   Mean   : 0.00   Mean   :0.47   Mean   :0.13  
 3rd Qu.: 0.53   3rd Qu.:1.00   3rd Qu.: 0.520   3rd Qu.: 0.52   3rd Qu.:1.00   3rd Qu.:0.00  
 Max.   : 3.09   Max.   :1.00   Max.   : 3.145   Max.   : 4.07   Max.   :1.00   Max.   :1.00

Hierarchical clustering: hclust()

Distance

1
2
3
4
5
6
7
8
9
> seg.dist <- dist(seg.df.sc) 

> as.matrix(seg.dist)[1:5, 1:5]
         1        2        3        4        5
1 0.000000 1.885319 1.786323 2.139937 2.225970
2 1.885319 0.000000 1.245679 2.705915 2.883670
3 1.786323 1.245679 0.000000 2.463979 2.936121
4 2.139937 2.705915 2.463979 0.000000 1.762212
5 2.225970 2.883670 2.936121 1.762212 0.000000

Clustering

1
2
> seg.hc <- hclust(seg.dist, method="complete") 
> plot(seg.hc)

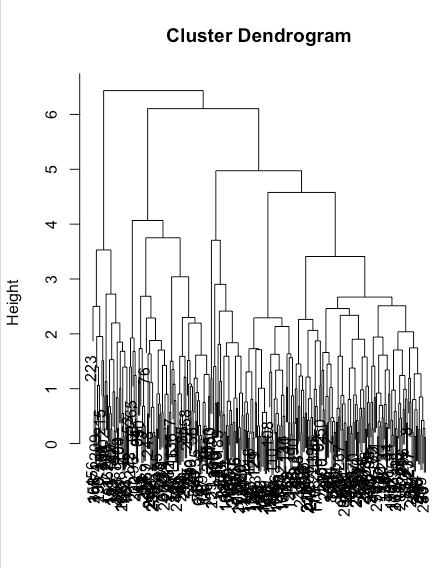
hclust(d, method = “complete”)

d：数据的距离矩阵或相似度矩阵。距离矩阵是一个对称矩阵，其中每个元素表示两个观测点之间的距离。相似度矩阵也是一个对称矩阵，其中每个元素表示两个观测点之间的相似度。通常可以使用 dist() 函数计算距离矩阵或相似度矩阵。
method：指定用于计算簇间距离的方法。常用的方法包括：

“single”：最短距离法（single linkage）。
“complete”：最远距离法（complete linkage）。
“average”：平均距离法（average linkage）。
“ward.D”：Ward’s 方法，通过最小化簇内方差来合并簇。

hclust() 函数返回一个树形结构对象（dendrogram），可以使用 plot() 函数对其进行可视化。通过调整 method 参数，可以控制聚类的方式以及簇间的相似性度量。

1
> plot(cut(as.dendrogram(seg.hc), h = 4)$lower[[1]])

1
2
3
4
5
6
7
8
9
> seg.df[c(156, 152),] #similar
         age gender   income kids ownHome subscribe
156 66.89691      0 54060.59    0       1         0
152 64.45890      0 61052.08    0       1         0

> seg.df[c(156, 183),] #less similar
         age gender    income kids ownHome subscribe
156 66.89691      0  54060.59    0       1         0
183 57.79006      1 105537.82    0       1         0

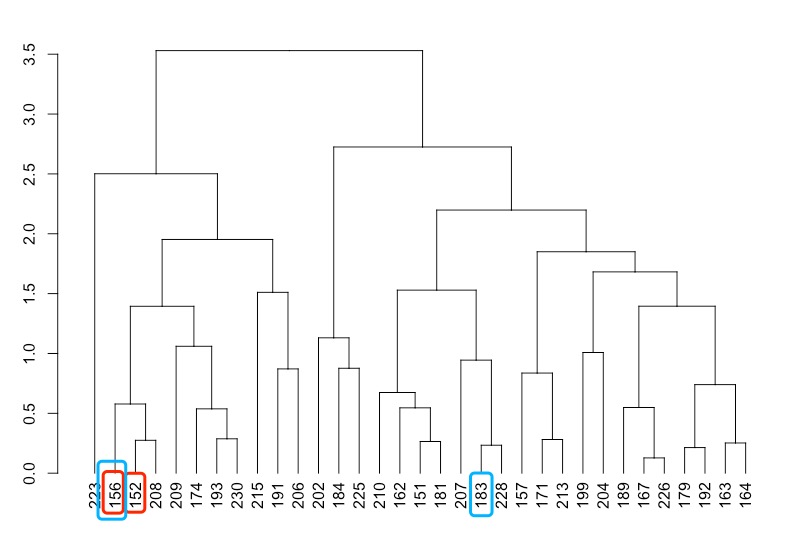
as.dendrogram()

将不同的对象转换为树形结构对象。它可以接受多种不同的输入对象，包括：

hclust 对象：从 hclust() 函数返回的聚类结果对象。
agnes 对象：从 agnes() 函数返回的聚类结果对象。
phylo 对象：从 ape 包中的函数返回的系统发育树对象。
dist 对象：距离矩阵对象，表示观测点之间的距离或相似度。

使用 as.dendrogram() 函数可以将以上这些对象转换为 dendrogram 对象，然后可以使用 dendrogram 对象进行可视化、分析或其他操作。

Getting groups

1
2
3
> plot(seg.hc)

> rect.hclust(seg.hc, k=4, border = "red")

1
2
3
4
5
6
> seg.hc.segment <- cutree(seg.hc, k=4) #membership vector for 4 groups 

> table(seg.hc.segment) #counts
seg.hc.segment
  1   2   3   4 
164  73  30  33

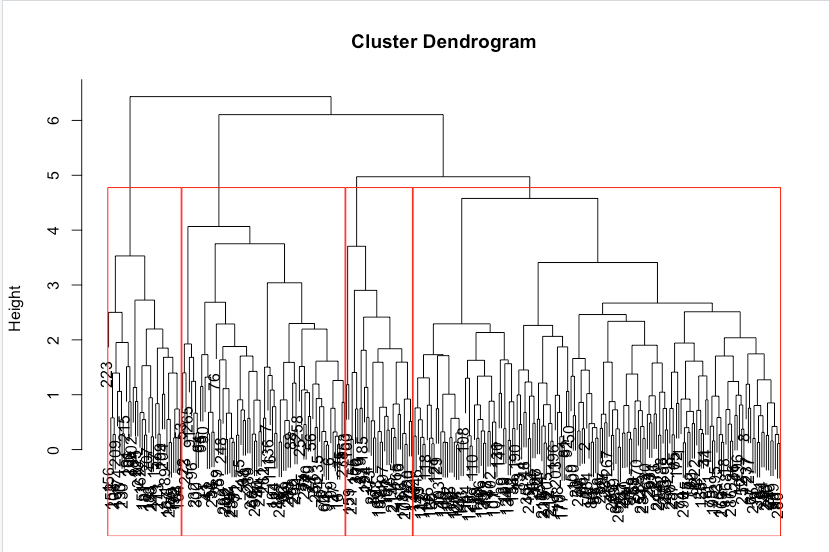
Describing clusters

1
2
3
4
5
6
7
8
library(cluster) 
clusplot(seg.df, seg.hc.segment,
         color = TRUE, #color the 
         lines = 0, #omit distance lines between groups
         main = "Hierarchical cluster plot", # figure title
         groupsshade = TRUE, #shade the ellipses for group membership 
         labels = 4, #label only the groups, not the individual points 
)

1
2
3
4
5
6
> aggregate(seg.df, list(seg.hc.segment), mean)
  Group.1      age    gender   income     kids   ownHome  subscribe
1       1 35.70250 0.5121951 45474.72 0.847561 0.3292683 0.15243902
2       2 37.34969 0.5479452 54571.75 3.273973 0.4520548 0.08219178
3       3 57.61221 0.6333333 40589.64 0.100000 0.9333333 0.16666667
4       4 62.11487 0.4242424 79444.84 0.000000 0.7878788 0.12121212

1
boxplot(seg.df$income ~ seg.hc.segment, ylab = "Income", xlab = "Cluster")

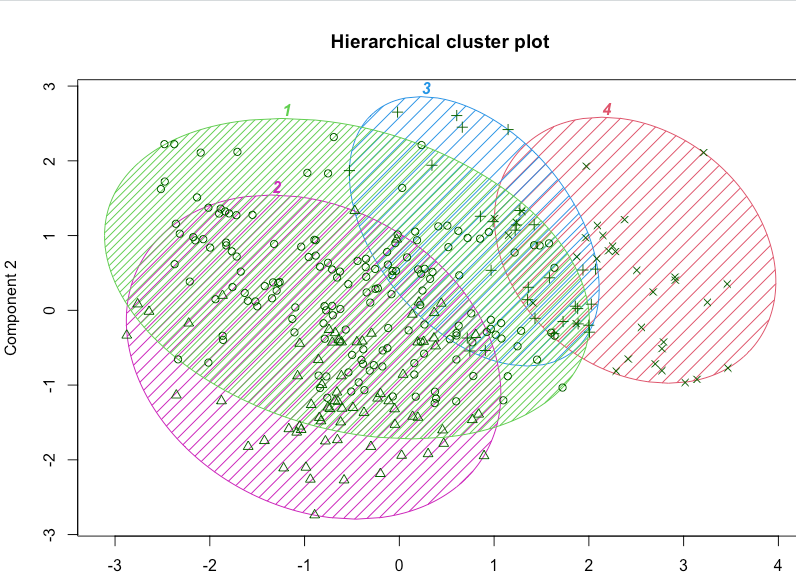
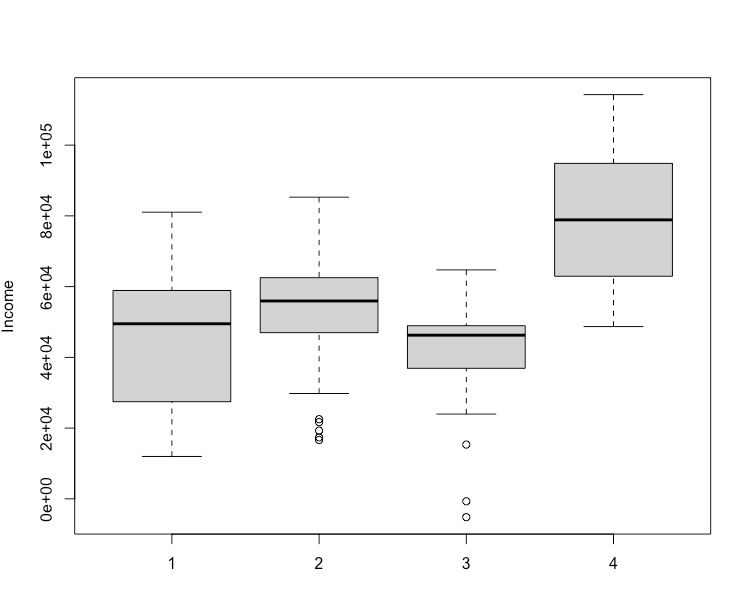
boxplot()

绘制箱线图，是一种常用的统计图形，用于显示一组数据的分布情况，包括中位数、四分位数、极值等。

箱线图

箱线图（Boxplot）是一种常用的统计图形，用于显示一组数据的分布情况。它提供了关于数据分布、中心位置、离散程度和异常值等方面的直观信息。箱线图通常包括以下几个部分：

箱子（Box）：箱子由两条水平线段组成，分别表示数据的上四分位数（Q3）和下四分位数（Q1）。箱子的中间线表示数据的中位数（Q2）。
须（Whiskers）：须延伸出箱子的两端，通常由直线或线段表示。须的长度通常是箱子高度的1.5倍的四分位距（IQR = Q3 - Q1）。须的端点通常是最大非异常值和最小非异常值，但具体的定义可能因数据分布而异。
异常值（Outliers）：在箱子的须之外的数据点被视为异常值，并单独绘制出来，通常以圆圈或星号表示。

箱线图的绘制过程通常涉及以下步骤：

计算数据的描述性统计量，包括最小值、最大值、中位数、四分位数等。
根据计算的描述性统计量绘制箱子和须。
根据数据中的异常值绘制异常值。
添加额外的注释和标签，使得图形更加清晰易懂。

箱线图可以用于比较不同组之间的数据分布情况，检测异常值，以及观察数据的离散程度。它是一种简洁而有效的可视化工具，适用于各种类型的数据分析和探索。

Mean-based clustering: kmeans()

Clustering

1
2
> set.seed(96743)
> seg.k <- kmeans(seg.df.sc, centers = 4) #use standardized variables

Describing clusters

1
2
3
4
5
6
> aggregate(seg.df, list(seg.k$cluster), mean)
  Group.1      age    gender   income       kids   ownHome  subscribe
1       1 26.12680 0.3728814 21850.99 1.16949153 0.2542373 0.16949153
2       2 59.86977 0.5522388 66319.07 0.02985075 0.7611940 0.08955224
3       3 38.10768 0.6136364 56864.13 2.96590909 0.4772727 0.11363636
4       4 40.15887 0.5116279 52841.06 0.56976744 0.3837209 0.16279070

1
boxplot(seg.df$income ~ seg.k$cluster, ylab = "Income", xlab = "Cluster")

1
2
3
4
5
6
7
clusplot(seg.df, seg.k$cluster,
         color = TRUE,
         shade = TRUE,
         labels = 4,
         lines = 0,
         main = "K_means cluster plot",
)

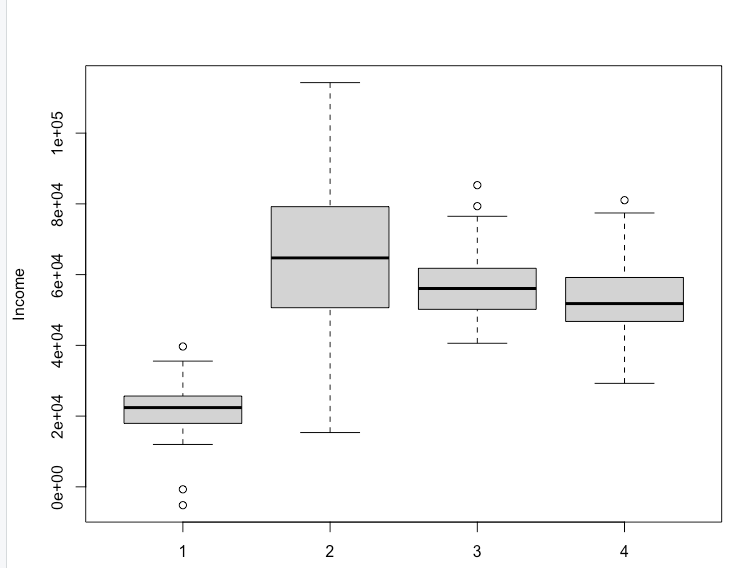
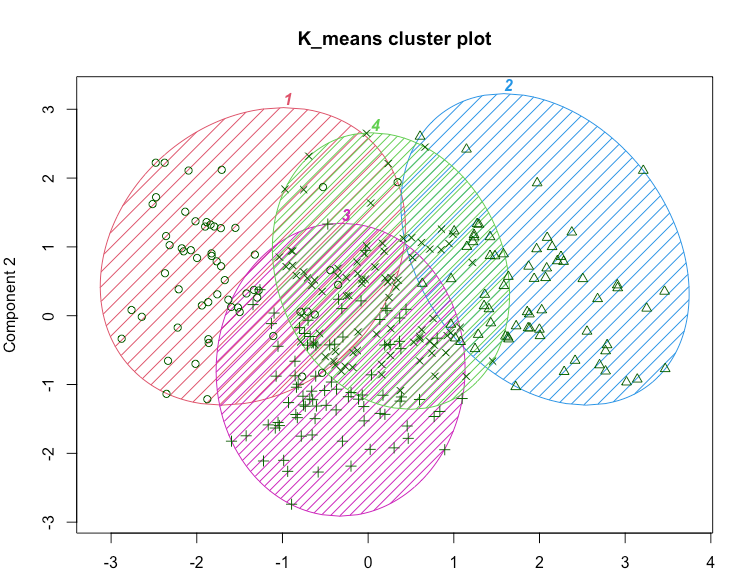
这可能暗示了一种商业策略。在当前情况下，例如，我们看到第二组在一定程度上有所区别，并且拥有最高的平均收入。这可能使其成为潜在宣传活动的良好目标。还有许多其他策略可供选择；关键点在于分析提供了值得考虑的有趣选项。

k-means分析的一个局限性是需要指定聚类的数量，并且很难确定一个解决方案是否比另一个更好。如果我们要对当前的问题使用k-means，我们将重复分析k=3、4、5等，并确定哪个解决方案对我们的业务目标最有用。

Model-based clustering: Mclust()

关键思想是观察结果来自具有不同统计分布（例如不同的均值和方差）的群体。算法试图找到最佳的一组这样的潜在分布，以解释观察到的数据。

Clustering

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
> library(mclust) #install if needed

> seg.mc <- Mclust(seg.df.sc) 

> summary(seg.mc)
---------------------------------------------------- 
Gaussian finite mixture model fitted by EM algorithm 
---------------------------------------------------- 

Mclust VEV (ellipsoidal, equal shape) model with 3 components: 

 log-likelihood   n df       BIC       ICL
      -1291.139 300 73 -2998.655 -2998.655

Clustering table:
  1   2   3 
163  71  66

结果显示，数据被估计为具有三个大小不同的聚类，如表所示。
我们还看到对数似然信息，我们可以用它来比较模型。例如，我们尝试一个四个聚类的解决方案。

对数似然（log-likelihood）是统计学中用于评估模型拟合优良度的一种常用指标。它通常用于描述一个模型对观测数据的拟合程度有多好。对数似然值越高，表示模型对观测数据的拟合越好。

具体来说，对数似然值是在给定模型参数的条件下，观测数据出现的概率的对数。对于给定的观测数据集，我们可以将观测数据视为从一个概率分布中独立地抽取得到的样本。然后，对数似然值表示了在给定模型参数的条件下，观测数据出现的可能性大小。对数似然值越高，表示观测数据出现的可能性越大，即模型拟合效果越好。

在实际应用中，对数似然值通常用于比较不同模型的拟合效果。我们可以对同一组观测数据使用不同的模型进行拟合，并计算每个模型的对数似然值。然后，通过比较对数似然值的大小，我们可以确定哪个模型对观测数据的拟合效果更好。

需要注意的是，对数似然值通常是负数。这是因为对数似然值是一个概率的对数，而概率的取值范围是0到1之间。因此，对数似然值越大，表示概率越接近于1，而对数似然值越小（即绝对值越大），表示概率越接近于0。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
> seg.mc4 <- Mclust(seg.df.sc, G =4) #specifying the number of clusters 
> summary(seg.mc4)

---------------------------------------------------- 
Gaussian finite mixture model fitted by EM algorithm 
---------------------------------------------------- 

Mclust VII (spherical, varying volume) model with 4 components: 

 log-likelihood   n df       BIC       ICL
      -1690.304 300 31 -3557.425 -3597.143

Clustering table:
  1   2   3   4 
 51  74 119  56 

看起来分为3组时，对数似然估计更高。

Comparing models

1
2
3
4
> BIC(seg.mc, seg.mc4)
        df      BIC
seg.mc  73 2998.655
seg.mc4 31 3557.425

3-cluster better.

Describing clusters

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
> aggregate(seg.df, list(seg.mc$classification), mean)
  Group.1      age    gender   income     kids   ownHome subscribe
1       1 44.68018 0.5276074 52980.52 1.171779 0.8650307 0.2453988
2       2 38.02229 1.0000000 51550.98 1.422535 0.0000000 0.0000000
3       3 36.02187 0.0000000 45227.51 1.348485 0.0000000 0.0000000

> library(cluster)

> clusplot(seg.df, seg.mc$classification, color = TRUE, shade = TRUE,
+          labels = 4, lines = 0, main = "Model-based cluster plot")

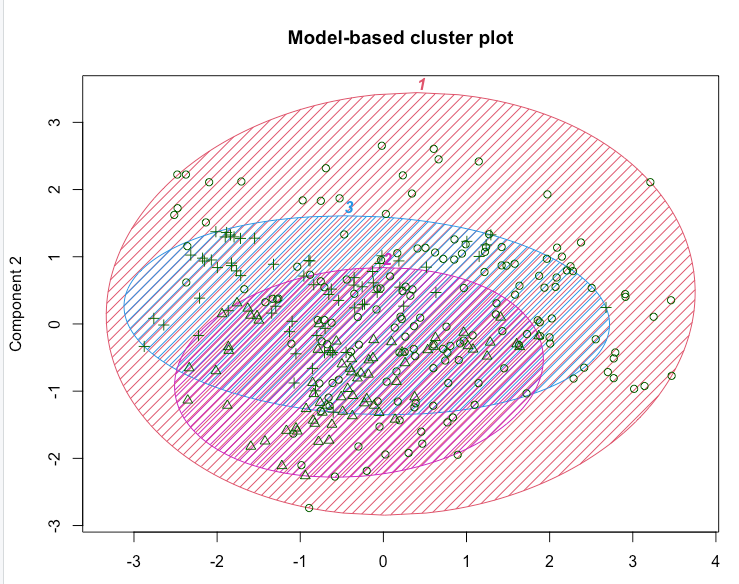
Week2 Code

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
## install.packages ("readxl")
## install.packages ("psych")
## install.packages ("car")
## install.packages ("gpairs")
## install.packages ("grid")
## install.packages ("lattice")
## install.packages ("corrplot")
## install.packages ("gplots")
## install.packages ("mclust")
## install.packages ("cluster")

library("readxl")
library("psych")
library("car")
library("gpairs")
library("grid")
library("lattice")
library("corrplot")
library("gplots")
library("mclust")
library("cluster")

## 获取当前已加载文件的目录
file_dir <- dirname(parent.frame(2)$ofile)
print(file_dir)
## 将工作目录设置为当前已加载文件的目录
setwd(file_dir)

seg.df <- read.csv("Data_Segmentation.csv", stringsAsFactors = TRUE)

head(seg.df, n=8)

seg.df$gender <- ifelse(seg.df$gender=="Male",0,1)
seg.df$ownHome <- ifelse(seg.df$ownHome == "ownNo", 0,1)
seg.df$subscribe <- ifelse(seg.df$subscribe == "subNo", 0,1)
head(seg.df)

seg.df.sc <- seg.df
seg.df.sc[, c(1,3,4)] <- scale(seg.df[, c(1,3,4)])
## We only need to standardize continuous variables.
head(seg.df.sc)

summary(seg.df.sc, digits = 2)

seg.dist <- dist(seg.df.sc) 
as.matrix(seg.dist)[1:5, 1:5]

seg.hc <- hclust(seg.dist, method="complete") 
seg.hc

plot(seg.hc)

plot(cut(as.dendrogram(seg.hc), h = 4)$lower[[1]])

seg.df[c(156, 152),] #similar
seg.df[c(156, 183),] #less similar

plot(seg.hc)
rect.hclust(seg.hc, k=4, border = "red")

seg.hc.segment <- cutree(seg.hc, k=4) #membership vector for 4 groups 
table(seg.hc.segment) #counts

library(cluster) 
clusplot(seg.df, seg.hc.segment,
         color = TRUE, #color the groups
         shade = TRUE, #shade the ellipses for group membership
         labels = 4, #label only the groups, not the individual points 
         lines = 0, #omit distance lines between groups
         main = "Hierarchical cluster plot" # figure title
)

aggregate(seg.df, list(seg.hc.segment), mean)

boxplot(seg.df$income ~ seg.hc.segment, ylab = "Income", xlab = "Cluster")

set.seed(96743)
seg.k <- kmeans(seg.df.sc, centers = 4) #use standardized variables

aggregate(seg.df, list(seg.k$cluster), mean)

boxplot(seg.df$income ~ seg.k$cluster, ylab = "Income", xlab = "Cluster")

clusplot(seg.df, seg.k$cluster,
         color = TRUE,
         shade = TRUE,
         labels = 4,
         lines = 0,
         main = "K_means cluster plot",
)

library(mclust) #install if needed
seg.mc <- Mclust(seg.df.sc) 
summary(seg.mc)

seg.mc4 <- Mclust(seg.df.sc, G =4) #specifying the number of clusters 
summary(seg.mc4)

BIC(seg.mc, seg.mc4)

aggregate(seg.df, list(seg.mc$classification), mean)
library(cluster)
clusplot(seg.df, seg.mc$classification, color = TRUE, shade = TRUE,
         labels = 4, lines = 0, main = "Model-based cluster plot")