R: 4.3.2 (2023-10-31) R studio: 2023.12.1+402 (2023.12.1+402)
- 了解为什么有效的营销策略必须管理客户动态:这部分强调了管理客户动态对于实现有效营销策略的重要性。
- 批判性地解释管理客户动态的主要方法:这部分详细解释了两种主要方法,即动态客户细分方法和客户生命周期价值方法。动态客户细分方法指的是将客户按照不同的动态特征进行分类,以便更好地满足其需求。客户生命周期价值方法则是通过分析客户在整个生命周期内的价值来指导营销策略。
- 使用分析工具:这部分提到了使用选择模型和客户生命周期价值分析等分析工具来支持上述方法的实施。
1. Customer Dynamics
客户对大多数产品和服务的需求随时间变化或由于特定事件而变化。
- 客户偏好随时间变化:因为个体消费者的需求随着年龄、经验或特定事件而改变,也可能是因为客户所处的行业或市场随着时间的推移发生了变化。
- 客户的需求变化不仅是由于人们之间的固有差异:还由于人们和市场的变化而引起。因此,我们需要根据客户的时间依赖性需求,而不是仅仅基于“通用”需求对所有客户进行“静态”的细分。
因此,客户动态是所有企业在制定有效营销策略时必须解决的基本“问题”。客户会发生变化;如果不能理解和解决这些动态,就会导致业务绩效不佳。
1.1 生命周期方法
使用通用的客户成长阶段及其在生命周期中的位置来确定客户偏好和相关策略。
- Customer lifecycle
- Product lifecycle
- Industry lifecycle
优点:
- 简单易懂:将所有客户都视为遵循同一曲线。
- 易于使用:对所有客户进行平均处理。
- 使用通用的客户生命周期阶段及其在生命周期中的位置来确定客户偏好和相关策略。
缺点:
- 忽略客户动态的原因。
- 仅适用于以离散阶段进行划分的情况,不适用于连续变化的情况。
1.2 动态客户细分
根据客户类似的获取、拓展和保留阶段对公司现有客户进行分段。
- 选择模型可以在所有获取、拓展和保留阶段进行分析,因为它预测了观察到的客户选择的可能性。
优点:
- 结合了生命周期和细分方法。
- 符合战略营销思维。
- 将持续变化转化为离散阶段。
缺点:
- 细分可能不是完全同质的。
- 无法精确匹配所有客户的特点。
1.3 客户生命周期价值
捕捉客户根据其预期迁移路径在整个与公司的生命周期中的贡献。
- 客户生命周期价值(CLV)分析使用折现现金流,并提供所有信息以做出最佳的获取、拓展和保留决策。
优点:
- 为AER(Acquisition-Expansion-Retention)决策提供洞察。
- 支持客户为中心的文化。
- 捕捉了客户根据其预期迁移路径在与企业的整个生命周期中的贡献。
缺点:
- 需要对未来迁移有深入的了解。
- 需要详细的财务数据。
- 忽略了动态和异质性。
2. Choice Model
Choice Model 试图确定不同因素(价格、促销)对消费者个体选择(加入、交叉购买、离开)的影响。它是最流行的个体级响应模型。
- 输入:
- 使用过去营销行动和与实际客户响应(选择)相关联的人口统计数据的数据库。
- 使用过去的行为数据;无需调查或获取客户输入(从过去客户的行为推断权重)。
- 输出
- 每个输入变量对结果的系数估计(例如,年龄、子女、信用和直邮对选择的影响)
- 客户选择的概率(升级销售、保留的概率,并可针对获取目标运行列表)
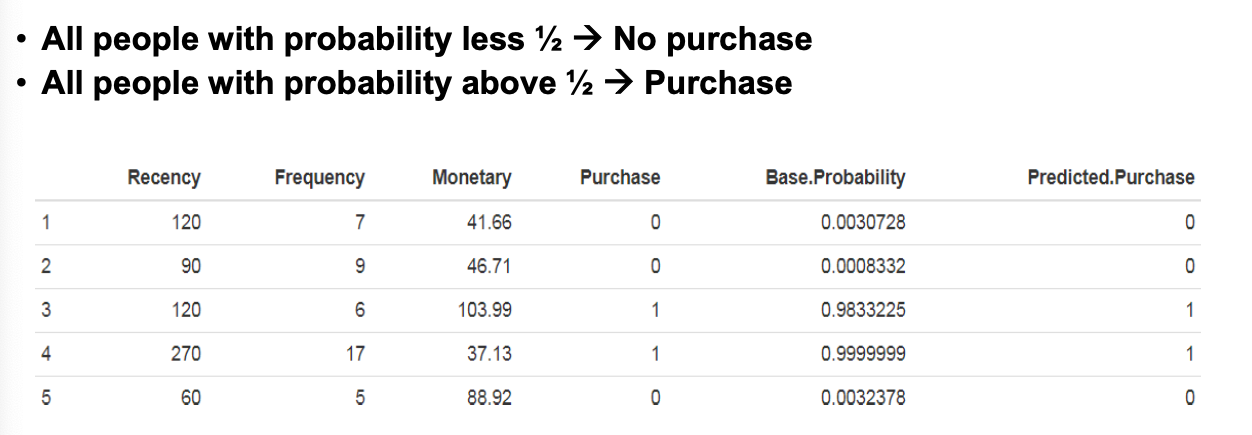
• 因变量:- 购买(是/否)
2.1 Generalised linear models (GLM) 广义线性模型
是一种统计模型,可以用于分析具有非正态误差结构的数据,例如二项分布、泊松分布等。GLM 是线性模型的一种扩展,它允许因变量和自变量之间的关系不是线性的,同时也不要求因变量服从正态分布。
-
Linear regression:线性回归,是一种用于建立因变量和一个或多个自变量之间的线性关系的统计方法。它假设因变量和自变量之间的关系是线性的,并尝试拟合一条直线来描述这种关系。
-
Logistic regression:逻辑回归,是一种用于建立因变量与一个或多个自变量之间的非线性关系的统计方法。逻辑回归用于分析因变量是二元变量的情况,它通过将线性回归模型的结果转换成概率来进行分类。
-
Multinomial logistic regression:多项式逻辑回归,是逻辑回归的一种扩展,适用于因变量有多个类别的情况。与二元逻辑回归不同,多项式逻辑回归可以处理多类别的因变量,并提供各类别的概率。
2.2 Binary choice: logistic regression
-
Response to marketing efforts:营销活动的反应。指客户在接收到营销活动后的反应,比如使用优惠券或电子邮件广告后是否购买了产品。
- Did the customer buy after being sent a coupon or an email ad?:客户在收到优惠券或电子邮件广告后是否购买了产品。
-
Online/Catalogue purchase (Buy/No-Buy):在线或目录购买。指客户在网上或通过目录购买产品的行为,以及是否购买了产品。
- Recency, Frequency, Monetary value (RFM) measures as predictors of purchase:最近购买时间、购买频率和购买金额(RFM)作为购买预测的指标。这些是用来预测客户是否会购买产品的指标。
Spend = ᵝ1Frequency + β0:这是线性回归模型的表达式,其中Spend是因变量(要预测的变量),Frequency是自变量(用来预测的变量),ᵝ1是Frequency的系数(也称为斜率),β0是截距。
-
The line slope: the effect of frequency on money spend:线的斜率表示Frequency对花费的影响,即每单位Frequency的变化导致花费的变化量。
-
The intercept: the money spend when frequency is 0:截距表示当Frequency为0时的花费,即在Frequency为0时的基础花费。
-
Linear regression uses the data to estimate ᵝ1 and ᵝ0:线性回归使用数据来估计ᵝ1和ᵝ0。
-
Spend = 0.5 Frequency + 0.6:这是一个线性回归模型的具体示例,其中斜率为0.5,截距为0.6。
-
Then using this regression model, we can predict the money spend given a frequency:然后,使用这个回归模型,我们可以根据给定的频率来预测花费。
2.2.1 公式
odd:购买概率 / 不购买的概率 $$ \text{odds} = \frac{Probability of purchase}{Probability of no-purchase} = \frac{p}{1-p} $$
qlogis() $$ \log (\frac{p}{1-p}) = \log(\text{odds}) $$
p(plogis):购买概率 $$ p = \frac{e^{\log(\text{odds})}}{1 + e^{\log(\text{odds})}} $$
odd / p 转换 $$ p = \beta_1 \text{frequency} + \beta_0 $$
$$ \log(\text{odds}) = \beta_1 \text{frequency} + \beta_0 $$
2.2.2 Odds and Choice Probability
Utility
$$ V_b = \log(\frac{p}{1-p}) $$
Odds
$$ \text{odds} = \exp(V_b) = \frac{p}{1-p} $$
Probability
$$ p = \frac{\exp(V_b)}{\exp(V_b) + 1} $$
$$ Utility from not buying: V_n = 0 $$
$$ Odds of buying: \exp(2) = e^2 = 7.39 $$
$$ Odds of not buying: \exp(0) = 1 $$
$$ Probability of buying: p = \frac{\exp(2)}{\exp(2) + 1} = \frac{7.39}{7.39 + 1} = \frac{7.39}{8.39} = 0.88 $$
-
模型表明,消费者对购买和不购买(保留钱)都有一定的效用:
- 购买的效用:$V_b$
- 不购买的效用:$V_n=0$
- 如果$V_b > V_n=0$,消费者就会购买。
-
对于RFM数据,购买的效用因RFM变量而异:
- $V_b = \beta_0 + \beta_1 \text{Recency} + \beta_2 \text{Frequency} + \beta_3 \text{Monetary}$
-
Logistic回归使用数据来估计模型参数(β系数)。
3. Example
3.1 数据
-
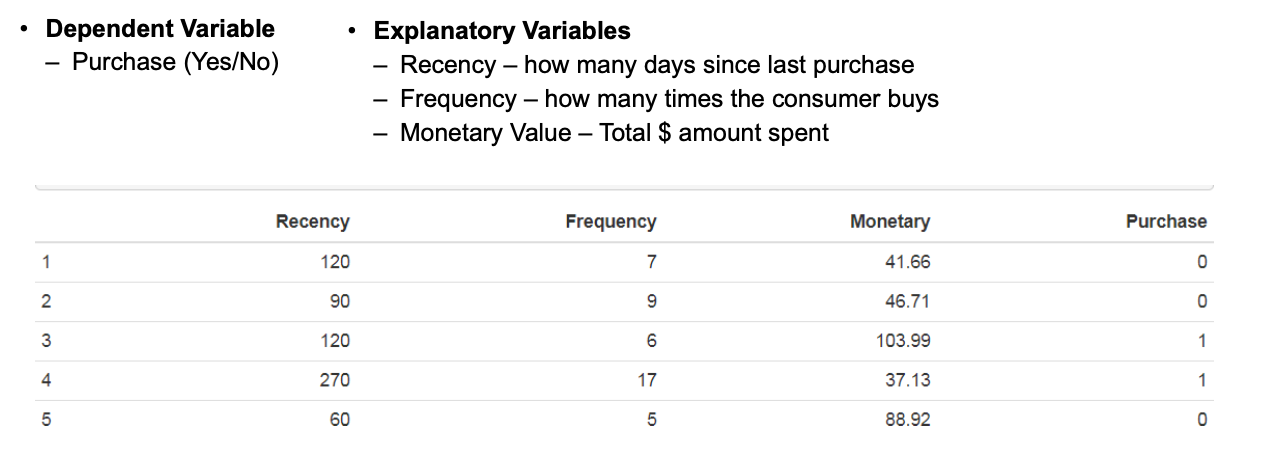
因变量:
- 购买(是/否)
-
解释变量:
- 最近购买距今多少天
- 消费者购买次数
- 总购买金额
3.2 logistic output
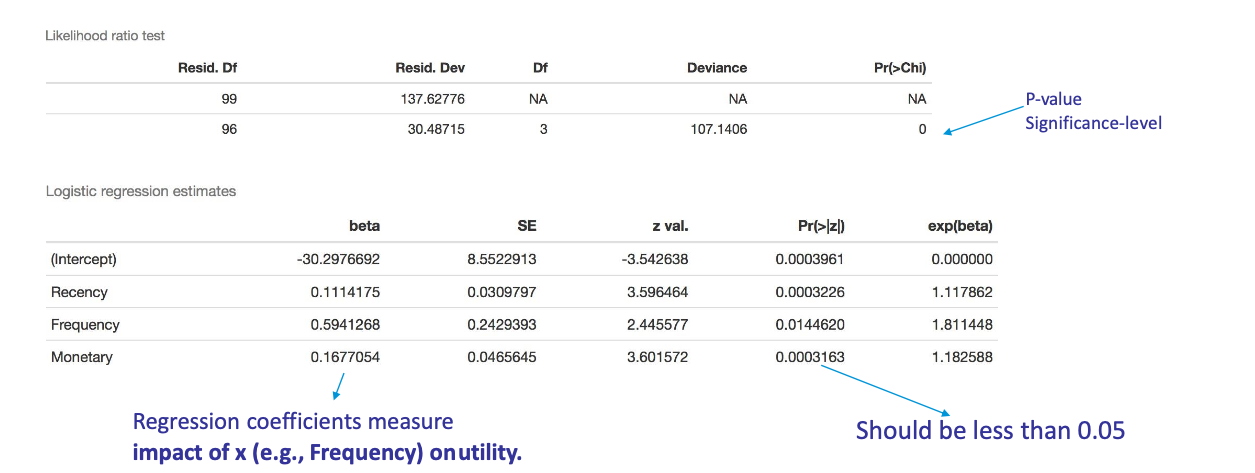
- Redis.Df:重新参数化的自由度,表示模型中参数的数量。
- Redis.Dev:重新参数化的偏差,表示模型与观察数据之间的偏差度量。
- Df Deviance:偏差的自由度,表示模型对观察数据的拟合程度。
- Pr(>Chi):卡方检验的p值,用于检验模型的拟合优度。它表示给定假设条件下,观察到的偏差和期望偏差之间的差异程度,从而判断- 模型是否对观察数据拟合良好。通常,p值越小,表示模型拟合得越好。
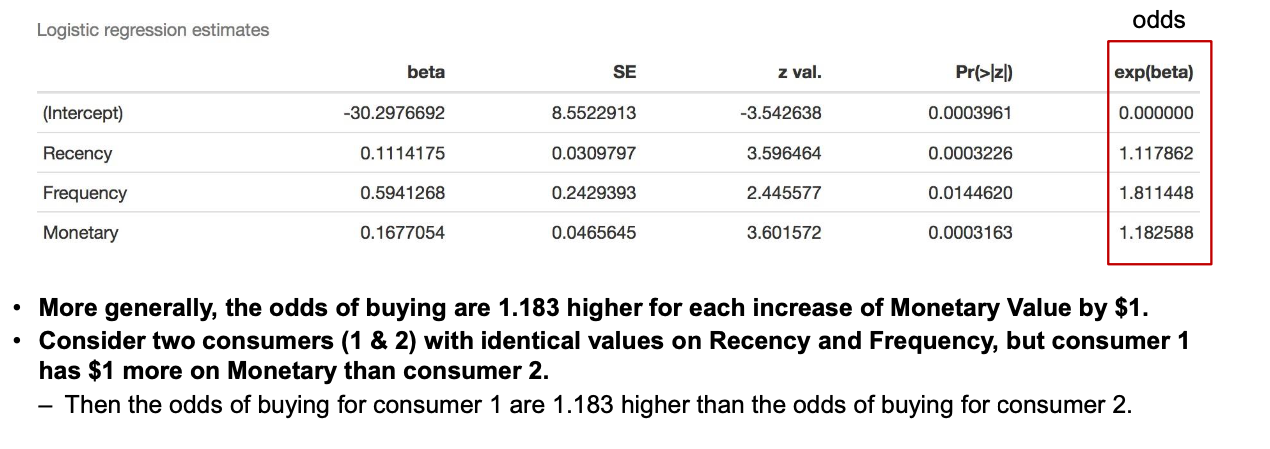
- intercept:在回归分析中,拟合的模型通常包括截距项(intercept),它代表了在所有自变量都为零时,因变量的预期值。这是模型中的一个重要部分,它确保了模型的灵活性,并使模型能够更好地拟合数据。在回归结果的输出中,"(intercept)"表示截距项的估计值和相关的统计信息。
- beta:模型参数的估计值,表示自变量对因变量的影响程度。
- SE:标准误差,表示估计的参数值与真实参数值之间的差异的标准偏差。它衡量了估计参数的不确定性。
- z val.:z值,表示模型参数估计值与零假设之间的偏差量(以标准误差为单位)。z值越大,表示参数估计值与零假设之间的偏差越大。
- Pr(>|z|):z检验的p值,用于检验模型参数的显著性。它表示模型参数是否显著不同于零假设。通常,p值小于0.05被认为是统计上显著的。
- exp(beta):参数的指数,表示自变量单位变化对因变量的影响的倍数。通常用于解释模型中的自变量对因变量的影响程度。
-
更一般地,每增加1美元的购买金额,购买的几率会增加1.183倍。
-
考虑两个消费者(1和2),他们的最近购买距今多少天和购买次数相同,但消费者1比消费者2的购买金额多1美元。
- 那么,消费者1购买的几率将比消费者2购买的几率高出1.183倍。
-
在 RFM 数据中估计的效用函数为: $$ V = -30.29 + 0.111 \times \text{Recency} + 0.594 \times \text{Frequency} + 0.168 \times \text{Monetary} $$
-
预测购买概率为: $$ p = \frac{\exp(V)}{\exp(V) + 1} $$
3.3 Lift Calculation
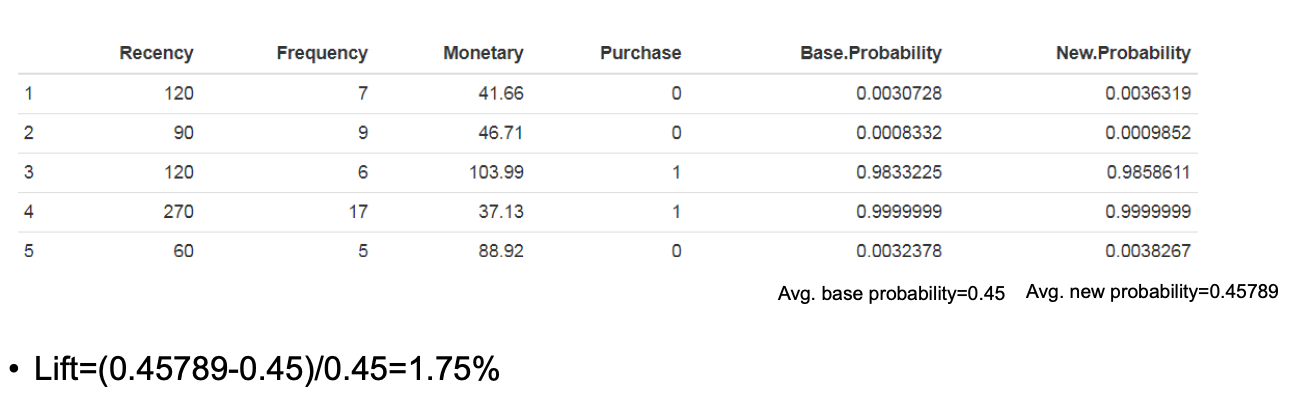
- 增加1美元购买金额对购买概率的影响:
- 计算购买新的效用值: $$ V_{\text{new}} = -30.29 + 0.111 \times \text{Recency} + 0.594 \times \text{Frequency} + 0.168 \times (\text{Monetary} + 1) $$
- 计算新的购买概率: $$ p_{\text{new}} = \frac{\exp(V_{\text{new}})}{\exp(V_{\text{new}}) + 1} $$
- 提升: $$ \text{Lift}{\text{new}} = \frac{\exp(V{\text{new}})}{\exp(V_{\text{base}}) + 1} - p_{\text{base}} $$ 其中,$ p_{\text{base}} $ 是基准购买概率。
3.4 Classification
3.5 Classification (Hit Rate)

- 准确率:命中率=(51+43)/100=94%
- 灵敏度:真正率=43/(43+2)=96%
- 特异度:真负率=51/(51+4)=93%
- 假阳率=1-93%=7%
准确率(Accuracy):分类正确的样本数与总样本数之比。它表示模型正确预测的样本比例。
灵敏度(Sensitivity,也称为真正率或召回率):真正例(正类样本)中被正确预测为正类的比例。它衡量了模型在正类样本中的识别能力。
特异度(Specificity,也称为真负率):真负例(负类样本)中被正确预测为负类的比例。它衡量了模型在负类样本中的识别能力。
假阳率(False Positive Rate):负类样本中被错误预测为正类的比例。它是特异度的补数,表示模型在负类样本中的错误识别率。
这些指标通常用于评估二分类模型(正类和负类)。在实际应用中,选择哪个指标取决于具体的业务需求和分类任务的重要性。
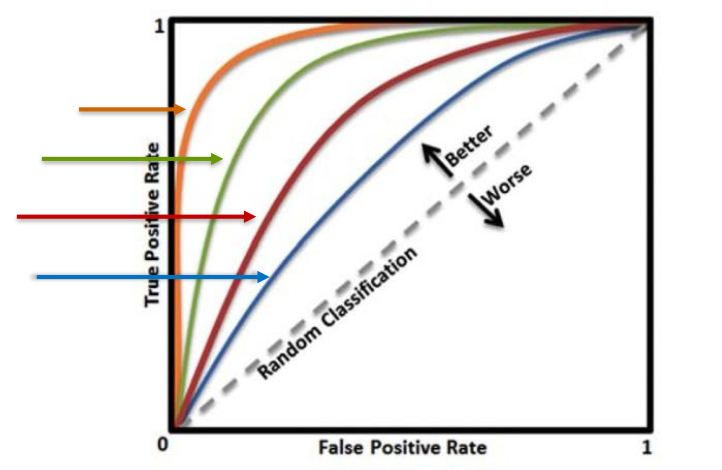
4. ROC (Receiver Operating Characteristic) Curve
这些是用于解释ROC曲线的AUC(曲线下面积)值的常见阈值:
- 大于0.9:优秀
- 0.8-0.9:良好
- 0.7-0.8:尚可
- 0.6-0.7:较差
ROC曲线是衡量二分类模型性能的重要工具,AUC值是ROC曲线下的面积,用于量化模型对正例和负例的区分能力。通常情况下,AUC值越高,模型性能越好。
5. Dynamic Segmentation
根据概率尺度从高到低对客户进行排名。针对以下客户:
- 属于前 X% 的顶尖客户(客户管理/资源分配)
- 概率高于某个阈值的客户(良好前景)
- 概率低于某个阈值的客户(即将“失去”的客户,营销仪表板)
- 这些方法可以帮助公司根据客户的概率分数进行优先级排序,并根据业务需求采取相应的行动。
6. Takeaway
选择模型是一种数学模型,用于预测观察到的客户选择的可能性,其受到公司营销的影响。选择建模在市场研究中非常普遍,用于理解各种消费者决策。
选择分析的两种常见方法有:
- 二项式逻辑回归用于二元选择
- 多项式逻辑模型用于选择集中超过两个备选项的情况。