R: 4.3.2 (2023-10-31)
R studio: 2023.12.1+402 (2023.12.1+402)

识别、管理客户的差异性

Agenda

  1. Framework
  2. Segmentation, Targeting, and Positioning (STP) Approach
  3. Analysis tools
  • Cluster analysis for segmentation
  • Factor analysis for developing perceptual maps

Perceptual Maps

在市场营销中，因子分析用于开发感知地图（Perceptual Maps）。感知地图是一种可视化工具，用于显示产品或品牌在消费者心中的位置，并显示与之相关的竞争对手。感知地图通常是二维图表，其中轴表示与产品相关的关键属性或特征，而各个产品或品牌则在图表上相应位置上显示。

因子分析在开发感知地图中的作用是帮助确定应该考虑哪些因素来区分产品或品牌之间的不同。它通过分析数据集中的变量之间的关系，确定潜在的因素或维度。这些因素或维度可以代表消费者在评估产品或品牌时所关注的重要特征。因子分析可以帮助识别潜在的共同因素，从而为感知地图的构建提供指导。

SWOT

SWOT分析（SWOT analysis）是一种用于评估组织、项目或个人的内部优势（Strengths）、内部劣势（Weaknesses）、外部机会（Opportunities）和外部威胁（Threats）的方法。这种分析通常用于制定战略计划、决策制定和问题解决过程中。

  1. 优势（Strengths）：组织或项目内部的积极因素和优势。这些可以包括资源、技能、声誉、市场地位等方面的优势。
  2. 劣势（Weaknesses）：组织或项目内部的负面因素和劣势。这些可能是缺乏某些资源、技能不足、管理问题等内部挑战。
  3. 机会（Opportunities）：外部环境中有利于组织或项目发展的因素。这些可能是市场趋势、技术进步、竞争对手的弱点等。
  4. 威胁（Threats）：外部环境中可能对组织或项目构成风险和威胁的因素。这些可能是竞争加剧、法规变化、市场需求下降等。

SWOT分析的目的是帮助组织或个人识别其所面临的内部和外部因素，并基于这些因素制定战略，利用优势应对机会，克服劣势避免威胁。这种分析通常以四个象限的形式呈现，将优势和劣势放置在水平轴上，将机会和威胁放置在垂直轴上，以便更直观地了解它们之间的关系。

因子分析（Factor analysis）：

因子分析是一种统计技术，用于理解观察到的变量之间的潜在结构或模式。它试图找到一组潜在的因素（或维度），这些因素可以解释变量之间的共同变异性。在因子分析中，变量被假设是由一组潜在因素所影响，而这些潜在因素无法直接观察到。因子分析可用于简化数据集、识别变量之间的模式以及探索变量之间的关系。

聚类分析（Cluster analysis）：

聚类分析是一种无监督学习方法，用于将数据集中的对象分成相似的组或簇。在聚类分析中，目标是通过测量对象之间的相似性，将它们划分为具有高内部一致性和低组间一致性的组。聚类分析的结果是一组簇，每个簇内的对象彼此相似，而不同簇之间的对象则具有较大的差异。聚类分析可用于发现数据集中的隐藏模式、识别潜在的群组或者简化复杂的数据集。

GE矩阵（GE Matrix）：

GE矩阵，也称为General Electric矩阵或GE多重业务矩阵，是一种战略规划工具，用于评估公司的业务组合并决定资源分配。该矩阵通常由两个维度组成：市场吸引力和竞争力。市场吸引力通常用于评估行业的吸引力程度，而竞争力则用于评估公司在特定市场上的竞争力。通过将不同的业务单元或产品定位在GE矩阵的不同象限中，管理者可以更好地了解哪些业务单元需要进一步发展、保持、撤退或收缩，并制定相应的战略计划。

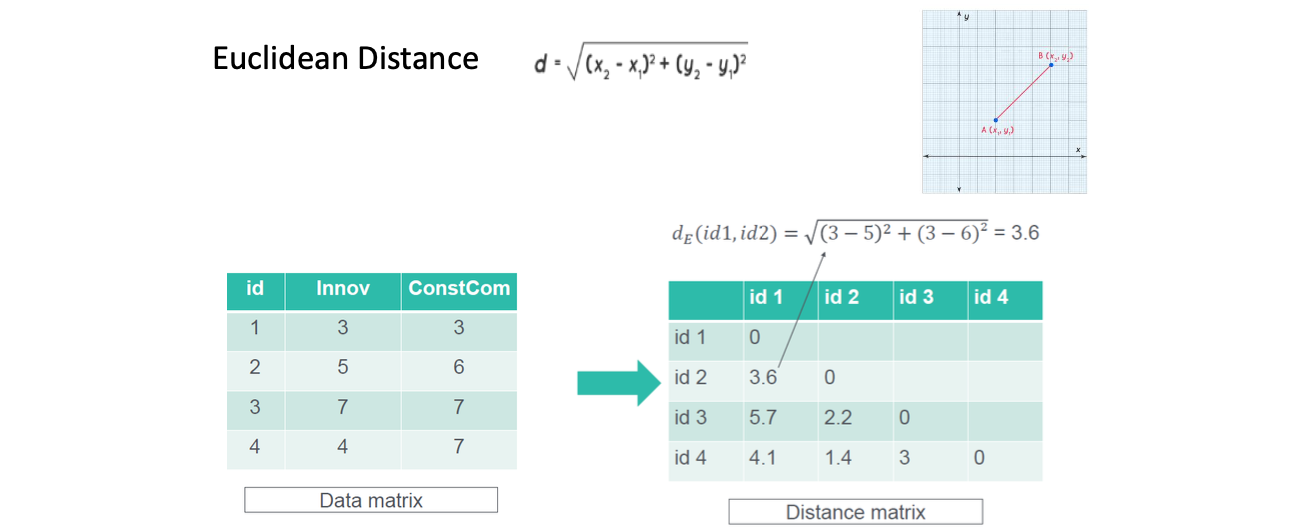
欧几里得距离 Euclidean Distance

欧几里得距离（Euclidean distance）是空间中两点之间的直线距离，通常用于衡量多维空间中的点之间的相似性或差异性。其含义是基于欧几里得几何学中的距离定义而来，即两点之间的直线最短路径的长度。

$$ d_e = \sqrt{\sum_{i=1}^{n}(x_i - y_i)^2} $$

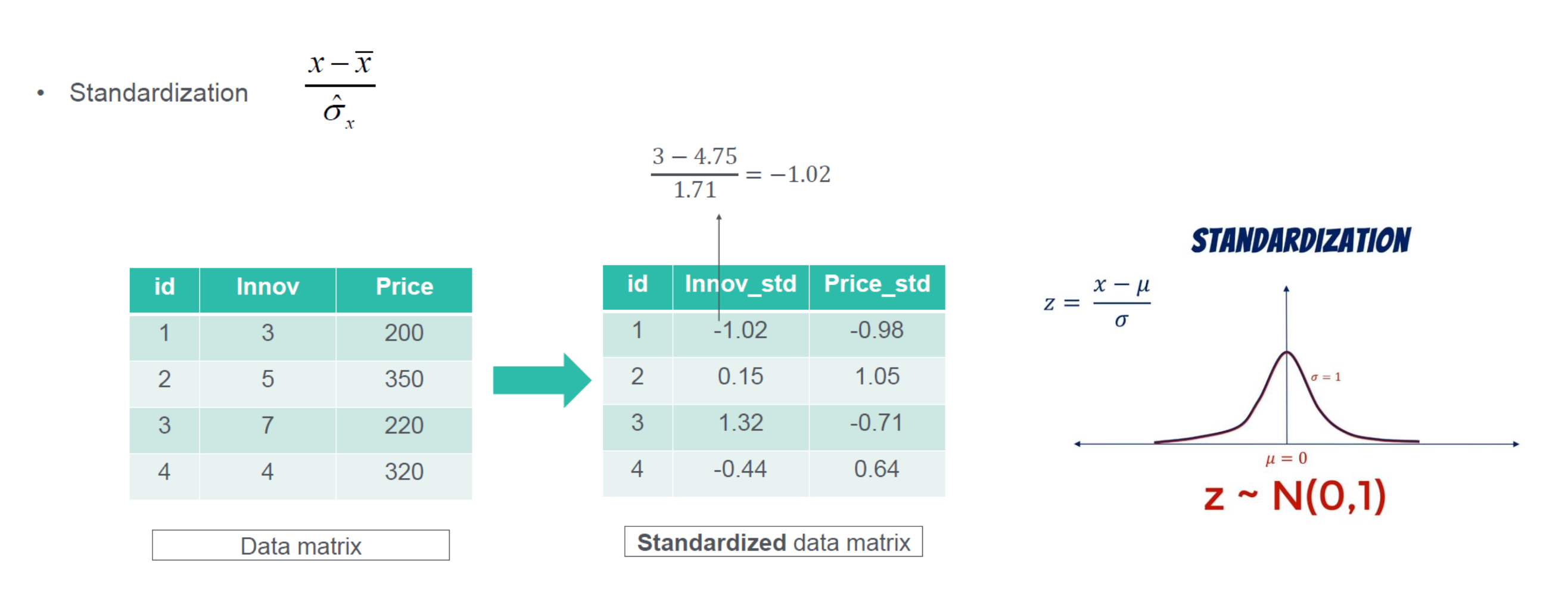
标准化 standardization

标准化的过程是将原始数据进行平移和缩放，使得数据的均值变为0，标准差变为1。这有助于消除不同变量之间的尺度差异，使得它们可以更好地进行比较和分析。

$$ z = \frac{x - \mu}{\sigma} $$

其中：

  • z：标准化后的值。
  • x：原始数据点的值。
  • μ：数据的均值，表示整个数据集的中心位置。
  • σ：数据的标准差，表示数据分布的离散程度或波动程度。

$$ \sigma = \sqrt{\frac{\sum_{i=1}^{n}(x_i - \mu)^2}{n}} $$

层次聚类 Hierarchical clustering

  • 单链接聚类（Single Linkage Clustering）：也称为最小距离法，它将两个簇之间的最近点之间的距离作为簇间距离的度量。

  • 完全链接聚类（Complete Linkage Clustering）：也称为最大距离法，它将两个簇中最远点之间的距离作为簇间距离的度量。

  • 平均链接聚类（Average Linkage Clustering）（Centroid Method）：它将两个簇中所有点对之间的平均距离作为簇间距离的度量。

  • 平均-平均链接聚类（Average-Average Linkage Clustering）：它结合了平均链接和平均-平均聚类的思想，利用两个簇中所有点对之间的平均距离作为簇间距离的度量。

  • 最大-最小平均链接聚类（Maximum-Minimum Average Linkage Clustering）：它结合了最大距离法和最小距离法的思想，将两个簇中最远点之间的距离和最近点之间的距离的平均值作为簇间距离的度量。

  • Ward Method：最小化簇内变异性或簇内点到质心的平方偏差和，它试图通过考虑每个点与其所属簇的质心之间的差异的平方和来最小化合并簇时的方差。

K-means clustering

K-means clustering 是一种基于距离的聚类方法，其目标是将数据点分成预先指定数量的簇，使得簇内的数据点相互之间的距离尽可能小，而不同簇之间的距离尽可能大。K-means 算法首先随机选择 k 个初始质心，然后迭代地将数据点分配到最近的质心，并更新质心的位置，直到达到收敛条件。K-means 的主要缺点是对于不同大小、密度和形状的簇表现不佳，并且对于初始质心的选择敏感。然而，K-means 是一种高效的算法，通常在大规模数据集上表现良好。

Model-based clustering

Model-based clustering 是一种基于概率模型的聚类方法，其主要思想是假设数据是由多个潜在的概率分布生成的混合物。这些分布通常是高斯分布或其变体，每个分布代表一个簇。模型基于这些概率分布的参数进行参数化，然后使用EM算法或其他优化方法对这些参数进行估计。在聚类时，通过最大化数据的似然性或最小化一个适当的损失函数来确定数据点的分配和模型参数。Model-based clustering 的优点包括能够处理不规则形状的簇以及能够估计每个数据点属于每个簇的概率。