本篇主要讲了利用R语言进行数据简单处理分析,和图表的绘制。
R: 4.3.2 (2023-10-31)
install and import libraries
# install.packages ("readxl") # install.packages ("psych") # install.packages ("car") # install.packages ("gpairs") # install.packages ("grid") # install.packages ("lattice") # install.packages ("corrplot") # install.packages ("gplots") library("readxl") library("psych") library("car") library("gpairs") library("grid") library("lattice") library("corrplot") library("gplots")
一、Data
1. vectors
# 导入数据 > store.df <- read.csv("Data_Descriptive.csv", stringsAsFactors=TRUE) > str(store.df) 'data.frame': 2080 obs. of 10 variables: $ storeNum: int 101 101 101 101 101 101 101 101 101 101 ... $ Year : int 1 1 1 1 1 1 1 1 1 1 ... $ Week : int 1 2 3 4 5 6 7 8 9 10 ... $ p1sales : int 127 137 156 117 138 115 116 106 116 145 ... $ p2sales : int 106 105 97 106 100 127 90 126 94 91 ... $ p1price : num 2.29 2.49 2.99 2.99 2.49 2.79 2.99 2.99 2.29 2.49 ... $ p2price : num 2.29 2.49 2.99 3.19 2.59 2.49 3.19 2.29 2.29 2.99 ... $ p1prom : int 0 0 1 0 0 0 0 0 0 0 ... $ p2prom : int 0 0 0 0 1 0 0 0 0 0 ... $ country : Factor w/ 7 levels "AU","BR","CN",..: 7 7 7 7 7 7 7 7 7 7 ... # 从上面结果可以看出,csv中一共有2080个观察值(行),10个变量(列)。 # 其中country是factor类型的,一共有7个level。
2. Summarize a single variable
2.1 Discrete variables
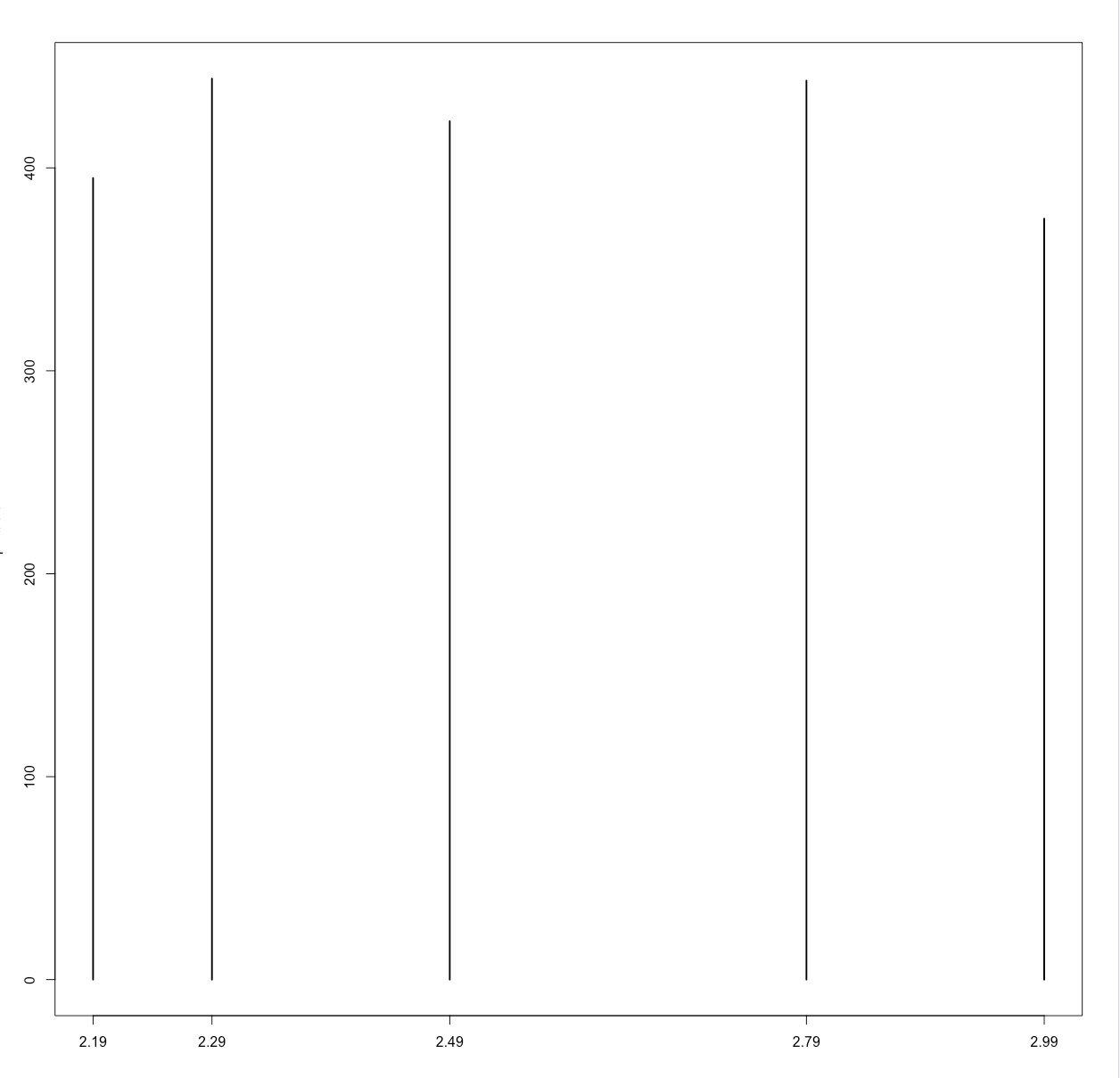
> table(store.df$p1price) 2.19 2.29 2.49 2.79 2.99 395 444 423 443 375
注⚠️:table() 函数
> df <- data.frame( + gender = c("Male", "Female", "Female", "Male", "Male", "Female", "Male", "Female", "Female", "Male"), + age_group = c("Young", "Young", "Old", "Young", "Old", "Young", "Old", "Old", "Young", "Young") + ) # 创建多维频数表 > table(df$gender, df$age_group) Young Old Female 3 2 Male 4 1
除table()外,还有其他类似的函数以及功能:
函数
描述
prop.table()
计算表格中每个单元格的比例。
xtabs()
创建频数表,支持多维数据和公式语法。
addmargins()
向表格中添加边际总计。
ftable()
创建扁平的表格,更容易查看和理解。
summary()
通常用于摘要统计,显示每个因子变量的数量,以及数值型变量的摘要统计量。
dplyr::count()
计算数据框中每个类别的频数,并返回包含频数的数据框。
psych::describe()
生成包含多个统计指标的摘要统计信息,如均值、标准差、最小值、最大值等。
题外话结束,继续前面的数据分析
> p1.table <- table(store.df$p1price) > p1.table 2.19 2.29 2.49 2.79 2.99 395 444 423 443 375 # talbe()返回的是一个table类型的结果 > str(p1.table) 'table' int [1:5(1d)] 395 444 423 443 375 - attr(*, "dimnames")=List of 1 ..$ : chr [1:5] "2.19" "2.29" "2.49" "2.79" ... # 转为图 > plot(p1.table)
注⚠️:plot()函数
用于创建各种类型的图形的基本函数之一。它可以用于绘制散点图、线图、柱状图、箱线图等等。后面会有更多的用法,就不在此处列举了。
# 二维table,获取每个价位上的促销频数 > table(store.df$p1price, store.df$p1prom) 0 1 2.19 354 41 2.29 398 46 2.49 381 42 2.79 396 47 2.99 343 32 # 计算product 1在每个price上的促销比例[prod1/(prod1+prod2)] > p1.table2 <- table(store.df$p1price, store.df$p1prom) > p1.table2[ ,2] / (p1.table2[ ,1] + p1.table2[ ,2]) 2.19 2.29 2.49 2.79 2.99 0.10379747 0.10360360 0.09929078 0.10609481 0.08533333
2.2 Continuous variables
注⚠️:Continuous variables VS Discrete variable
连续变量,指的是可以在一个范围内取任意值的变量,而不是一组离散的值。这种变量可以在某个范围内连续地取值,可以是任何数值。
离散变量,是指只能取有限个数值的变量。
对于连续变量,根据其分布来总结数据更有帮助。最常见的方法是使用数学函数来描述数据的范围、中心、集中或分散的程度,以及可能感兴趣的具体点(如第90百分位):
Describe
Function
Value
Extremes[极值]
min(x)
Min
max(x)
Max
Central trendency[中心趋势]
mean(x)
Arithmetic mean
median(x)
Mid
Dispersion[离散度]
var(x)
Variance around the mean
sd(x)
Standard deviaion(sqrt(var(x)))
IQR(x)
Interquartile range, 75th-25th percentile
mad(x)
Median absolute deviation
Points[观察值/数据点]
quantile(x, probs=c(…))
Percentiles
方差 var(x)
标准差 sd(x)
IQR(x)
mad(x)
IQR(Interquartile Range):
定义 :IQR是数据集中第三四分位数(Q3)和第一四分位数(Q1)之间的距离。计算方法 :IQR = Q3 - Q1,其中Q3是数据集中75th百分位数,Q1是数据集中25th百分位数。用途 :IQR通常用于识别数据中的离群值,因为它提供了数据中间50%的范围,并且对于偏斜分布的数据比标准差更鲁棒。
定义 :MAD是数据点与数据集中位数的绝对偏差的中位数。计算方法 :首先计算每个数据点与数据集中位数的绝对偏差,然后取这些绝对偏差的中位数。用途 :MAD也用于度量数据的离散程度,并且在处理离群值时更具有鲁棒性,因为它不受极端值的影响,类似于IQR。
IQR 和 MAD 相比:
计算方法 :IQR是基于四分位数计算的,而MAD是基于中位数计算的。
鲁棒性 :IQR和MAD都是鲁棒的统计量,对异常值的影响较小,但在某些情况下,MAD可能更为鲁棒,特别是当数据集包含大量离群值时。
解释 :IQR更容易解释,因为它代表了数据集中间50%的范围,而MAD则表示数据点与中位数的典型偏差。
常见用途 :IQR和MAD在异常值检测和数据分析中都很常见,但在不同的背景下可能有不同的应用场景。
quantile(x, probs=c(…))
x:包含数据的向量或数据框。
返回值:返回一个包含计算得到的分位数的向量,其顺序与 probs 中指定的顺序相对应。
# 创建一个示例数据集 > data <- c(10, 15, 20, 25, 30, 35, 40, 45, 50) # 计算第一四分位数、中位数、第三四分位数 > quantiles <- quantile(data, probs = c(0.25, 0.5, 0.75)) # 打印结果 > print(quantiles) 25% 50% 75% 20 30 40
题外话结束。
> min(store.df$p1sales) [1] 73 > max(store.df$p1sales) [1] 263 > mean(store.df$p1prom) [1] 0.1 > median(store.df$p2sales) [1] 96 > var(store.df$p1sales) [1] 805.0044 > sd(store.df$p1sales) [1] 28.3726 > IQR(store.df$p1sales) [1] 37 > mad(store.df$p1sales) [1] 26.6868 > quantile(store.df$p1sales, probs = c(0.25, 0.5, 0.75)) 25% 50% 75% 113 129 150
For skewed and asymmetric distributions that are common in marketing, such as unit sales or household income, the arithmetic mean() and standard deviation sd() may be misleading; in those cases, the median() and the interquartile range IQR() (the range of the middle 50% of data) are often used to summarize a distribution.
对于市场营销中常见的倾斜和不对称分布,例如单位销售或家庭收入,算术平均值()和标准差sd()可能会产生误导;在这些情况下,中位数()和四分位数间距IQR()(中间50%数据的范围)通常用于总结分布。
因为在偏斜和不对称分布的情况下,数据中可能存在极端值(离群值),这些值对于算术平均值和标准差的影响较大,导致这两个统计量可能不太准确地反映整体数据的特征。
算术平均值的问题: 偏斜分布中的极端值会对平均值产生较大的影响,使其偏离数据集的中心趋势。这导致平均值可能不再是数据的典型中心度量。
标准差的问题: 标准差对极端值非常敏感,因为它是基于平方差的,这会放大离群值的影响。这样,标准差可能高估了数据的真实分散程度。
相比之下,中位数是数据集中的中间值,不受极端值的影响,因此更能反映数据的中心趋势。四分位数间距(IQR)是数据中间50%的范围,它也对离群值具有一定的鲁棒性,因此更适合在偏斜分布中度量数据的分散程度。
综合起来,为了更准确地摘要和理解偏斜分布的数据特征,使用中位数和四分位数间距通常是更合适的选择。这样的度量方法更具有鲁棒性,能够提供更稳健、不受极端值干扰的数据摘要。
> quantile(store.df$p1sales, probs = c(0.05, 0.95)) # central 90% data 5% 95% 93 184 > quantile(store.df$p1sales, probs = 0:10/10) 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% 73.0 100.0 109.0 117.0 122.6 129.0 136.0 145.0 156.0 171.0 263.0o > quantile(store.df$p1sales, probs = seq(from=0, to=1, by=0.1)) 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100% 73.0 100.0 109.0 117.0 122.6 129.0 136.0 145.0 156.0 171.0 263.0
Suppose we wanted a summary of the sales for product 1 and product 2 based on their median and interquartile range. We might assemble these summary statistics into a data frame that is easier to read than the one-line- at-a-time output above. We create a data frame to hold our summary statistics. We name the columns and rows and fill in the cells with function values:
假设我们想根据产品1和产品2的中位数和四分位数范围汇总它们的销售额。我们可以将这些汇总统计信息组合成一个数据帧,这样比上面的一行一行的输出更容易阅读。我们创建一个数据框架来保存汇总统计数据。我们为列和行命名,并用函数值填充单元格:
mysummary.df <- data.frame(matrix(NA, nrow=2, ncol=2)) # 2 by 2 empty matrix names(mysummary.df) <- c("Median Sales", "IQR") # name columns rownames(mysummary.df) <- c("Product 1", "Product 2") # name rows mysummary.df["Product 1", "Median Sales"] <- median(store.df$p1sales) mysummary.df["Product 2", "Median Sales"] <- median(store.df$p2sales) mysummary.df["Product 1", "IQR"] <- IQR(store.df$p1sales) mysummary.df["Product 2", "IQR"] <- IQR(store.df$p2sales) mysummary.df
3 Summarize data frames
3.1 summary()
有事没事,summary一下
> summary(store.df) storeNum Year Week p1sales p2sales p1price p2price p1prom p2prom country Min. :101.0 Min. :1.0 Min. : 1.00 Min. : 73 Min. : 51.0 Min. :2.190 Min. :2.29 Min. :0.0 Min. :0.0000 AU:104 1st Qu.:105.8 1st Qu.:1.0 1st Qu.:13.75 1st Qu.:113 1st Qu.: 84.0 1st Qu.:2.290 1st Qu.:2.49 1st Qu.:0.0 1st Qu.:0.0000 BR:208 Median :110.5 Median :1.5 Median :26.50 Median :129 Median : 96.0 Median :2.490 Median :2.59 Median :0.0 Median :0.0000 CN:208 Mean :110.5 Mean :1.5 Mean :26.50 Mean :133 Mean :100.2 Mean :2.544 Mean :2.70 Mean :0.1 Mean :0.1385 DE:520 3rd Qu.:115.2 3rd Qu.:2.0 3rd Qu.:39.25 3rd Qu.:150 3rd Qu.:113.0 3rd Qu.:2.790 3rd Qu.:2.99 3rd Qu.:0.0 3rd Qu.:0.0000 GB:312 Max. :120.0 Max. :2.0 Max. :52.00 Max. :263 Max. :225.0 Max. :2.990 Max. :3.19 Max. :1.0 Max. :1.0000 JP:416 US:312 > summary(store.df$Year) Min. 1st Qu. Median Mean 3rd Qu. Max. 1.0 1.0 1.5 1.5 2.0 2.0 > summary(store.df, digits = 2) # 保留小数点后两位 storeNum Year Week p1sales p2sales p1price p2price p1prom p2prom country Min. :101 Min. :1.0 Min. : 1 Min. : 73 Min. : 51 Min. :2.2 Min. :2.3 Min. :0.0 Min. :0.00 AU:104 1st Qu.:106 1st Qu.:1.0 1st Qu.:14 1st Qu.:113 1st Qu.: 84 1st Qu.:2.3 1st Qu.:2.5 1st Qu.:0.0 1st Qu.:0.00 BR:208 Median :110 Median :1.5 Median :26 Median :129 Median : 96 Median :2.5 Median :2.6 Median :0.0 Median :0.00 CN:208 Mean :110 Mean :1.5 Mean :26 Mean :133 Mean :100 Mean :2.5 Mean :2.7 Mean :0.1 Mean :0.14 DE:520 3rd Qu.:115 3rd Qu.:2.0 3rd Qu.:39 3rd Qu.:150 3rd Qu.:113 3rd Qu.:2.8 3rd Qu.:3.0 3rd Qu.:0.0 3rd Qu.:0.00 GB:312 Max. :120 Max. :2.0 Max. :52 Max. :263 Max. :225 Max. :3.0 Max. :3.2 Max. :1.0 Max. :1.00 JP:416 US:312
在统计学中,“1st Qu” 和 “3rd Qu” 分别代表第一四分位数和第三四分位数。四分位数是将数据集分为四等份的值,它们用于描述数据分布的位置和分散程度。
第一四分位数(1st Qu)
是数据集中所有数值排序后第25%位置的值,也就是数据中的较小的四分之一。
第三四分位数(3rd Qu)
是数据集中所有数值排序后第75%位置的值,也就是数据中的较大的四分之三。
3.2 describe()
> library(psych) # install if needed > describe(store.df) vars n mean sd median trimmed mad min max range skew kurtosis se storeNum 1 2080 110.50 5.77 110.50 110.50 7.41 101.00 120.00 19.0 0.00 -1.21 0.13 Year 2 2080 1.50 0.50 1.50 1.50 0.74 1.00 2.00 1.0 0.00 -2.00 0.01 Week 3 2080 26.50 15.01 26.50 26.50 19.27 1.00 52.00 51.0 0.00 -1.20 0.33 p1sales 4 2080 133.05 28.37 129.00 131.08 26.69 73.00 263.00 190.0 0.74 0.66 0.62 p2sales 5 2080 100.16 24.42 96.00 98.05 22.24 51.00 225.00 174.0 0.99 1.51 0.54 p1price 6 2080 2.54 0.29 2.49 2.53 0.44 2.19 2.99 0.8 0.28 -1.44 0.01 p2price 7 2080 2.70 0.33 2.59 2.69 0.44 2.29 3.19 0.9 0.32 -1.40 0.01 p1prom 8 2080 0.10 0.30 0.00 0.00 0.00 0.00 1.00 1.0 2.66 5.10 0.01 p2prom 9 2080 0.14 0.35 0.00 0.05 0.00 0.00 1.00 1.0 2.09 2.38 0.01 country* 10 2080 4.55 1.72 4.50 4.62 2.22 1.00 7.00 6.0 -0.29 -0.81 0.04 # vars: 方差 # n: 观测数量(样本数量) # mean: 均值 # sd: 标准差 # median: 中位数 # trimmed: 修剪均值(去除异常值后的均值) # mad: 中位数绝对偏差(Median Absolute Deviation) # min: 最小值 # max: 最大值 # range: 范围(最大值与最小值的差) # skew: 偏度(Skewness,衡量分布偏斜程度) # kurtosis: 峰度(Kurtosis,衡量分布的尖峰程度) # se: 标准误差(Standard Error,均值的估计标准差) > describe(store.df[,c(2, 4:9)]) vars n mean sd median trimmed mad min max range skew kurtosis se Year 1 2080 1.50 0.50 1.50 1.50 0.74 1.00 2.00 1.0 0.00 -2.00 0.01 p1sales 2 2080 133.05 28.37 129.00 131.08 26.69 73.00 263.00 190.0 0.74 0.66 0.62 p2sales 3 2080 100.16 24.42 96.00 98.05 22.24 51.00 225.00 174.0 0.99 1.51 0.54 p1price 4 2080 2.54 0.29 2.49 2.53 0.44 2.19 2.99 0.8 0.28 -1.44 0.01 p2price 5 2080 2.70 0.33 2.59 2.69 0.44 2.29 3.19 0.9 0.32 -1.40 0.01 p1prom 6 2080 0.10 0.30 0.00 0.00 0.00 0.00 1.00 1.0 2.66 5.10 0.01 p2prom 7 2080 0.14 0.35 0.00 0.05 0.00 0.00 1.00 1.0 2.09 2.38 0.01
trimmed
trimmed 是指去除了数据中一定比例的极端值(通常是尾部的极端值)后计算得到的均值。修剪均值(trimmed mean)是一种对均值的修正,旨在减少极端值对均值的影响,从而更好地反映数据的中心趋势。
通常情况下,修剪均值的计算方式是将数据集中的一定比例的最小值和最大值去掉,然后计算剩余数据的算术平均值。这个比例可以根据实际情况而定,常见的修剪比例包括去掉5%、10%甚至更多的极端值。
修剪均值适用于数据集中存在明显的极端值或异常值的情况。与简单的算术平均值相比,修剪均值更加稳健,因为它对异常值的影响更小,更能够反映数据的典型中心位置。然而,需要注意的是,修剪均值可能会导致一定程度上的信息损失,尤其是当数据中的极端值具有特殊意义或重要性时。
mad
MAD(Median Absolute Deviation,中位数绝对偏差)是一种用于衡量数据集散布度的统计量,它衡量了数据点与数据集中位数之间的典型偏差。
具体而言,MAD是数据集中所有数据点与数据集中位数的绝对偏差的中位数。
MAD相对于标准差的优势在于它对极端值(离群值)具有较强的鲁棒性。因为MAD是基于绝对偏差的中位数计算的,它不受极端值的影响,更能够准确地描述数据的离散程度,尤其是在存在离群值的情况下。
MAD常用于金融领域和其他领域的数据分析中,特别是在需要考虑数据的异常值对结果的影响时。
Skewness(偏度)
是描述数据分布形态偏斜程度的统计量。它衡量了数据分布相对于其平均值的不对称性,即数据集在平均值两侧的分布是否对称。
正偏(Positive Skewness):数据分布向右偏移,尾部向右延伸,即数据集右侧的尾部较长,平均值右侧的数据点较多,形成一个长尾。正偏分布意味着数据集中存在较多较大的值。
负偏(Negative Skewness):数据分布向左偏移,尾部向左延伸,即数据集左侧的尾部较长,平均值左侧的数据点较多,形成一个长尾。负偏分布意味着数据集中存在较多较小的值。
偏度为0表示数据分布相对对称,大于0表示正偏,小于0表示负偏。偏度的绝对值越大,偏斜程度越明显。
偏度是了解数据分布形态的重要指标,特别是在做数据分析和模型建立时,它可以帮助我们判断数据集是否需要进行对称化处理,以满足建模的假设条件。
对称化处理是指通过某种方法或技术使数据分布更加对称的过程。在统计学和数据分析中,对称化处理通常用于调整数据的分布形态,使其更接近对称分布,以满足统计方法或模型的假设条件。 常见的对称化处理方法包括: 1. 对数转换(Log Transformation):对数转换是通过取数据的对数来减小数据的偏度。这种转换通常用于处理右偏分布的数据,将其转换为更接近对称分布的形式。 2. 方根转换(Square Root Transformation):方根转换是通过取数据的平方根来减小数据的偏度。类似于对数转换,它也可以用于调整右偏分布的数据。 3. 幂转换(Power Transformation):幂转换是通过取数据的某个幂次方来调整数据的分布形态。常见的幂次方包括0.5(平方根转换)、0.33、0.25等,具体选择取决于数据的分布特征。 4. 标准化(Standardization):标准化是将数据转换为均值为0,标准差为1的标准正态分布。虽然标准化不会改变数据的分布形态,但它可以将数据转换为具有固定均值和方差的形式,有助于在一些情况下比较不同尺度的变量。 对称化处理的目的是使数据更符合统计模型的假设,例如线性模型对数据的正态性假设。通过对数据进行对称化处理,可以提高统计分析的准确性和稳健性,并提高模型的拟合效果。
Kurtosis(峰度)
是描述数据分布峰态(尖峰程度)的统计量。它衡量了数据分布中数据点在均值附近聚集的程度,即数据集的尖峰度。
正峰(Positive Kurtosis):数据分布的峰态较高且尖锐,尾部较长。正峰分布表明数据集中的数据点在均值附近聚集得更为密集,同时存在更多的极端值,尾部更长。
负峰(Negative Kurtosis):数据分布的峰态较低且平缓,尾部较短。负峰分布表明数据集中的数据点分布更为扁平,相对更加分散。
正常的峰度为3。大于3的峰度表示分布尖峭(尖峰),而小于3的峰度表示分布平缓(扁平)。与偏度一样,峰度也是了解数据分布形态的重要指标,特别是在建模时需要考虑数据集的峰态特征。
se
se 代表的是标准误差(Standard Error)。标准误差是对样本统计量的抽样分布的离散程度进行估计的一种度量,用于衡量样本统计量与总体参数之间的差异。
在统计学中,标准误差通常用于估计样本统计量的抽样分布的离散程度,例如样本均值的标准误差用于估计样本均值的抽样分布的离散程度。标准误差越小,表示样本统计量更接近于总体参数的真值;标准误差越大,表示样本统计量与总体参数之间的差异越大。
标准误差的应用非常广泛,特别是在统计推断和假设检验中,它常用于计算置信区间、假设检验的统计量(如 t 统计量、z 统计量)
检查数据集的通用方法
read.csv 读取数据
转换为data frame,给定合适的名称
通过dim()检查是否是预期的行数和列数
> dim(store.df) [1] 2080 10
使用head()、tail()检查前几行和末尾几行,确保开头标题行和末尾空白行没有包含在内
> head(store.df) storeNum Year Week p1sales p2sales p1price p2price p1prom p2prom country 1 101 1 1 127 106 2.29 2.29 0 0 US 2 101 1 2 137 105 2.49 2.49 0 0 US 3 101 1 3 156 97 2.99 2.99 1 0 US 4 101 1 4 117 106 2.99 3.19 0 0 US 5 101 1 5 138 100 2.49 2.59 0 1 US 6 101 1 6 115 127 2.79 2.49 0 0 US > tail(store.df) storeNum Year Week p1sales p2sales p1price p2price p1prom p2prom country 2075 120 2 47 140 104 2.49 2.59 0 0 CN 2076 120 2 48 150 88 2.49 2.99 0 0 CN 2077 120 2 49 121 97 2.49 2.59 0 0 CN 2078 120 2 50 91 124 2.99 2.29 0 0 CN 2079 120 2 51 83 115 2.99 2.29 0 0 CN 2080 120 2 52 136 99 2.49 2.49 0 0 CN
使用Some()随机检查几行
> some(store.df) storeNum Year Week p1sales p2sales p1price p2price p1prom p2prom country 324 104 1 12 112 99 2.29 2.29 0 0 DE 644 107 1 20 131 92 2.49 2.59 0 0 DE 1032 110 2 44 211 70 2.19 3.19 0 1 GB 1183 112 1 39 155 80 2.29 2.59 1 0 BR 1274 113 1 26 121 117 2.29 2.29 0 0 BR 1518 115 2 10 157 82 2.49 3.19 0 0 JP 1525 115 2 17 167 72 2.49 3.19 0 0 JP 1565 116 1 5 186 63 2.19 3.19 0 0 JP 1974 119 2 50 144 111 2.99 3.19 0 0 CN 2036 120 2 8 125 103 2.79 2.99 0 0 CN
str()检查data frame架构,确保变量的类型和值是合适的,尤其是factor
> str(store.df) 'data.frame': 2080 obs. of 10 variables: $ storeNum: int 101 101 101 101 101 101 101 101 101 101 ... $ Year : int 1 1 1 1 1 1 1 1 1 1 ... $ Week : int 1 2 3 4 5 6 7 8 9 10 ... $ p1sales : int 127 137 156 117 138 115 116 106 116 145 ... $ p2sales : int 106 105 97 106 100 127 90 126 94 91 ... $ p1price : num 2.29 2.49 2.99 2.99 2.49 2.79 2.99 2.99 2.29 2.49 ... $ p2price : num 2.29 2.49 2.99 3.19 2.59 2.49 3.19 2.29 2.29 2.99 ... $ p1prom : int 0 0 1 0 0 0 0 0 0 0 ... $ p2prom : int 0 0 0 0 1 0 0 0 0 0 ... $ country : Factor w/ 7 levels "AU","BR","CN",..: 7 7 7 7 7 7 7 7 7 7 ...
7.summary()查看预期外的值,尤其是Min/Max
> summary(store.df) storeNum Year Week p1sales p2sales p1price p2price p1prom p2prom country Min. :101.0 Min. :1.0 Min. : 1.00 Min. : 73 Min. : 51.0 Min. :2.190 Min. :2.29 Min. :0.0 Min. :0.0000 AU:104 1st Qu.:105.8 1st Qu.:1.0 1st Qu.:13.75 1st Qu.:113 1st Qu.: 84.0 1st Qu.:2.290 1st Qu.:2.49 1st Qu.:0.0 1st Qu.:0.0000 BR:208 Median :110.5 Median :1.5 Median :26.50 Median :129 Median : 96.0 Median :2.490 Median :2.59 Median :0.0 Median :0.0000 CN:208 Mean :110.5 Mean :1.5 Mean :26.50 Mean :133 Mean :100.2 Mean :2.544 Mean :2.70 Mean :0.1 Mean :0.1385 DE:520 3rd Qu.:115.2 3rd Qu.:2.0 3rd Qu.:39.25 3rd Qu.:150 3rd Qu.:113.0 3rd Qu.:2.790 3rd Qu.:2.99 3rd Qu.:0.0 3rd Qu.:0.0000 GB:312 Max. :120.0 Max. :2.0 Max. :52.00 Max. :263 Max. :225.0 Max. :2.990 Max. :3.19 Max. :1.0 Max. :1.0000 JP:416 US:312
describe()查看各个item的n是否相同,并且检查trimmed和skew
> describe(store.df) vars n mean sd median trimmed mad min max range skew kurtosis se storeNum 1 2080 110.50 5.77 110.50 110.50 7.41 101.00 120.00 19.0 0.00 -1.21 0.13 Year 2 2080 1.50 0.50 1.50 1.50 0.74 1.00 2.00 1.0 0.00 -2.00 0.01 Week 3 2080 26.50 15.01 26.50 26.50 19.27 1.00 52.00 51.0 0.00 -1.20 0.33 p1sales 4 2080 133.05 28.37 129.00 131.08 26.69 73.00 263.00 190.0 0.74 0.66 0.62 p2sales 5 2080 100.16 24.42 96.00 98.05 22.24 51.00 225.00 174.0 0.99 1.51 0.54 p1price 6 2080 2.54 0.29 2.49 2.53 0.44 2.19 2.99 0.8 0.28 -1.44 0.01 p2price 7 2080 2.70 0.33 2.59 2.69 0.44 2.29 3.19 0.9 0.32 -1.40 0.01 p1prom 8 2080 0.10 0.30 0.00 0.00 0.00 0.00 1.00 1.0 2.66 5.10 0.01 p2prom 9 2080 0.14 0.35 0.00 0.05 0.00 0.00 1.00 1.0 2.09 2.38 0.01 country* 10 2080 4.55 1.72 4.50 4.62 2.22 1.00 7.00 6.0 -0.29 -0.81 0.04
番外 Trimmmed And Skewed
Trimmed
当数据集中存在极端值时,修剪均值可以更准确地反映数据的中心趋势。让我们通过一个具体的例子来说明这一点。
假设我们有一个包含10个观测值的数据集:
[ {2, 3, 4, 5, 6, 7, 8, 9, 10, 100} ]
这个数据集中有一个明显的极端值100。让我们计算一下这个数据集的简单算术平均值和修剪均值,并比较它们对数据中心趋势的反映。
首先,计算简单算术平均值:
$$
\text{Mean} = \frac{2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 100}{10} = 15.4
$$
接下来,我们计算修剪均值,剔除最大和最小的10%的观测值(即剔除一个极端值100):
$$
\text{Trimmed Mean} = \frac{3 + 4 + 5 + 6 + 7 + 8 + 9 + 10}{8} = 6.875
$$
从计算结果可以看出,简单算术平均值受到极端值100的影响,导致平均值达到了15.4,不够准确地反映了数据的中心趋势。而修剪均值剔除了极端值100后,得到的修剪均值为6.875,更接近数据的中心位置。
因此,通过比较简单算术平均值和修剪均值,我们可以更准确地了解数据的中心趋势,尤其是在数据集中存在极端值的情况下。
Skewed
当数据集中存在极端值时,数据的分布可能会偏斜(skewed),修剪均值可以在一定程度上减少极端值对数据的影响,从而改善数据分布的偏斜情况。
让我们继续使用上面的例子来说明修剪均值如何影响数据分布的偏斜情况。我们已经计算了简单算术平均值和修剪均值,现在我们将计算数据集的偏度(skewness),以了解修剪均值如何影响数据分布的偏斜性。
在R语言中,我们可以使用 psych 包中的 describe() 函数来计算数据集的偏度。让我们来进行计算:
install.packages( "psych" ) library( psych) data <- c ( 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 100 ) describe( data) $ skew
在这个例子中,数据集的偏度为4.07,这表明数据集是右偏(右偏的偏度值大于0)。右偏分布意味着数据集的尾部向右延伸,即数据集中存在极端值或较大的值。
现在,我们剔除极端值100,并重新计算数据集的偏度:
trimmed_data <- data[ data < 100 ] describe( trimmed_data) $ skew
剔除极端值后,修剪后的数据集的偏度为0.32。与原始数据集相比,修剪后的数据集的偏度更接近于0,表明修剪均值有助于减少数据分布的偏斜性,使数据更接近于对称分布。
因此,通过计算修剪均值和观察数据集的偏度,我们可以更好地理解极端值对数据分布的影响,以及修剪均值对于改善数据分布的偏斜性的作用。
3.3 apply()
apply(x = DATA, MARGIN = MARGIN, FUN = FUNCTION) apply(store.df[2:9], MARGIN = 1, FUN = mean) apply(store.df[2:9], MARGIN = 2, FUN = mean) apply(store.df[2:9], MARGIN = c(1,2), FUN = mean)
在 apply() 函数中,MARGIN 参数指定了函数应该沿着哪个维度(行或列)应用。MARGIN 参数可以取以下值:
MARGIN = 1:对每一行应用函数。MARGIN = 2:对每一列应用函数。MARGIN = c(1, 2):同时对每一行和每一列应用函数。
在给定的例子中,我们使用了 apply() 函数来对数据集 store.df 中的子集进行函数的应用,子集包含列索引为2到9的数据。具体解释如下:
apply(store.df[2:9], MARGIN = 1, FUN = mean):这句代码意味着对数据集 store.df 中的每一行(沿着行的方向)的列索引为2到9的数据应用 mean() 函数,计算每一行的平均值。
apply(store.df[2:9], MARGIN = 2, FUN = mean):这句代码意味着对数据集 store.df 中的每一列(沿着列的方向)的行索引为2到9的数据应用 mean() 函数,计算每一列的平均值。
apply(store.df[2:9], MARGIN = c(1,2), FUN = mean):这句代码意味着同时对数据集 store.df 中的每一行和每一列的行列交叉点(即所有的单元格)的数据应用 mean() 函数,计算所有行和列的平均值。
> apply(store.df[ 2:9], MARGIN = 2, FUN = mean) Year Week p1sales p2sales p1price p2price p1prom p2prom 1.5000000 26.5000000 133.0485577 100.1567308 2.5443750 2.6995192 0.1000000 0.1384615 > apply(store.df[ , 2:9], 2, sum) Year Week p1sales p2sales p1price p2price p1prom p2prom 3120.0 55120.0 276741.0 208326.0 5292.3 5615.0 208.0 288.0 > apply(store.df[ , 2:9], 2, sd) Year Week p1sales p2sales p1price p2price p1prom p2prom 0.5001202 15.0119401 28.3725990 24.4241905 0.2948819 0.3292181 0.3000721 0.3454668
4. Single variable visualisation
4.1 Histograms 柱状图
hist()
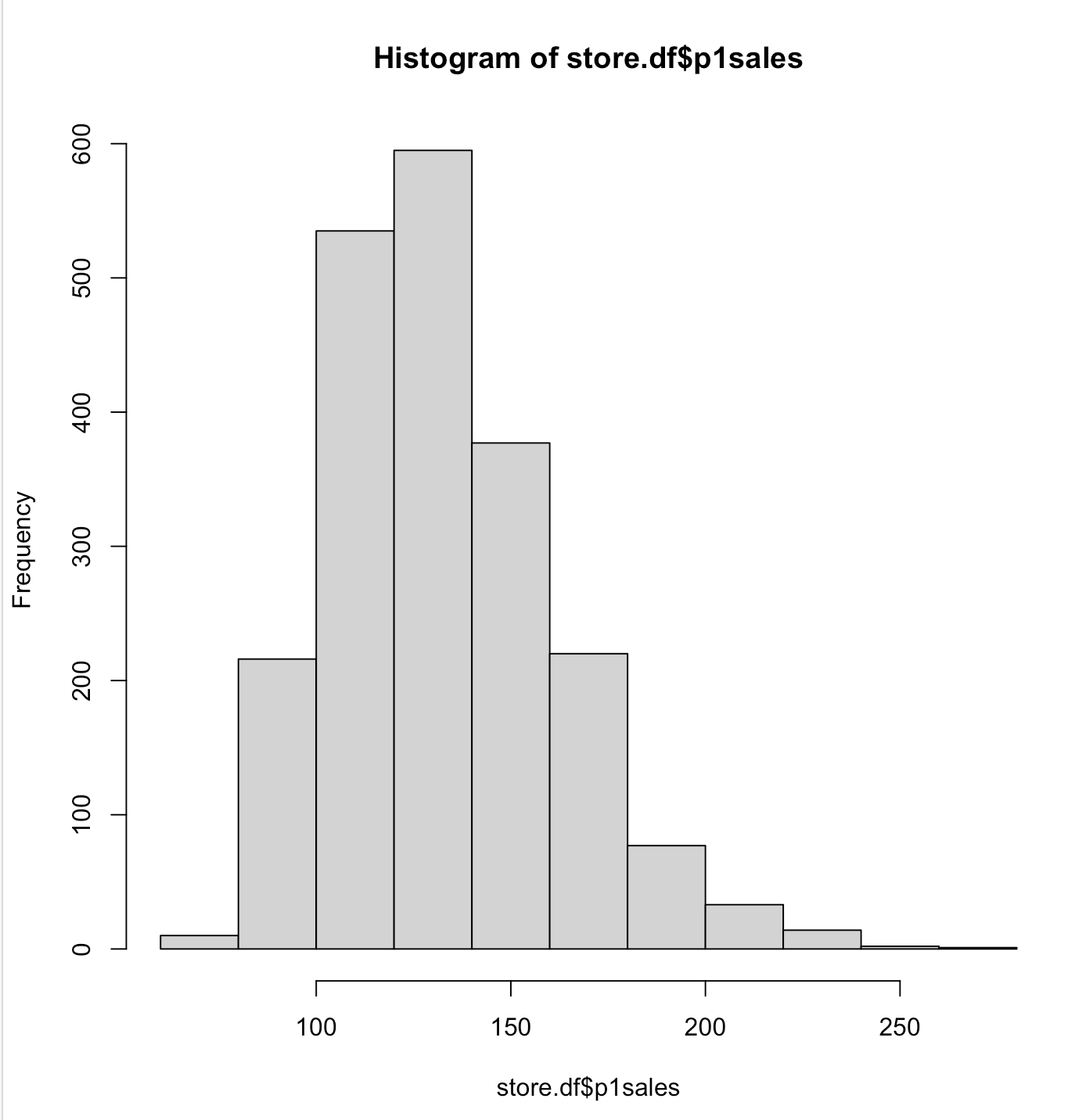
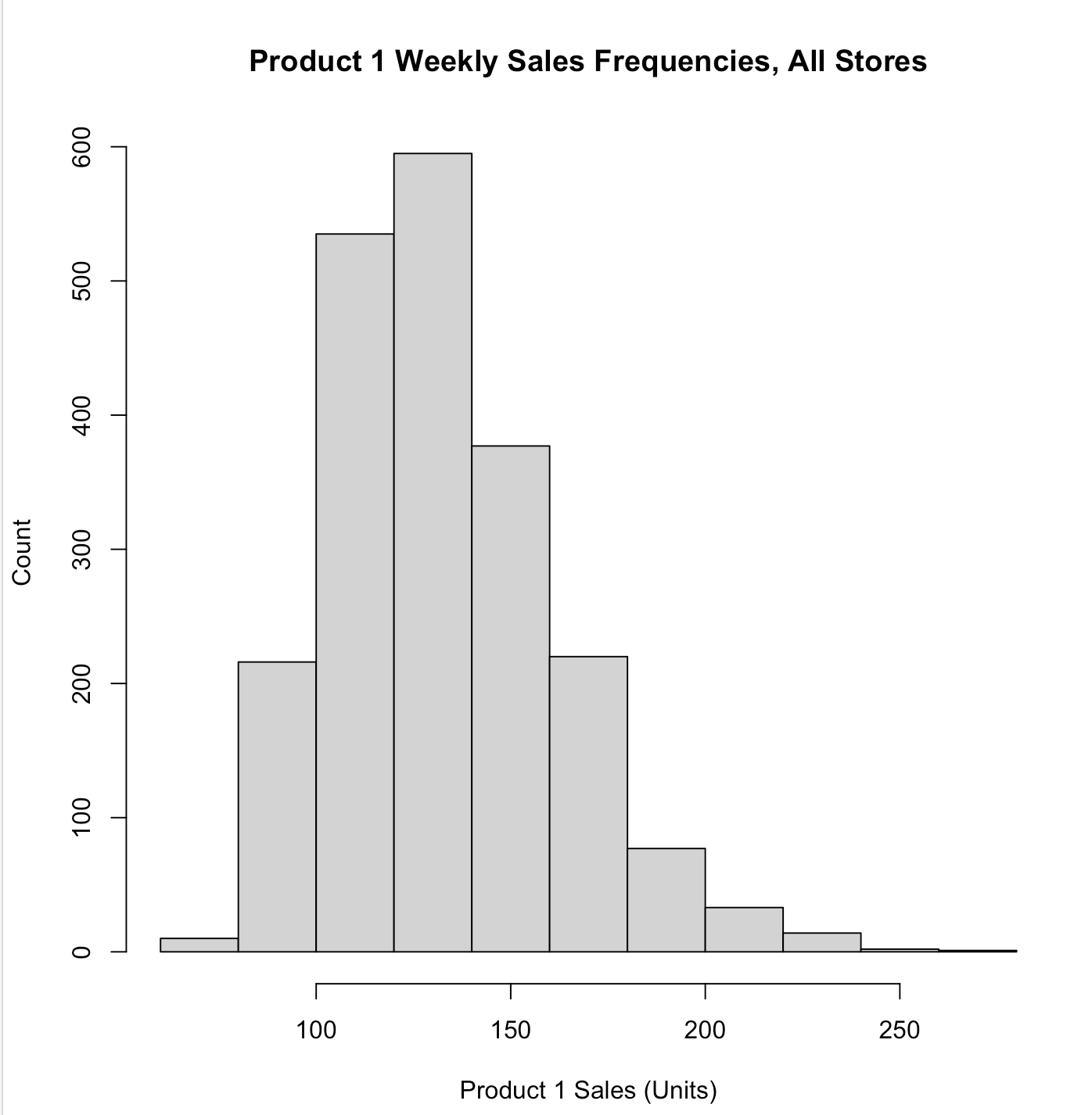
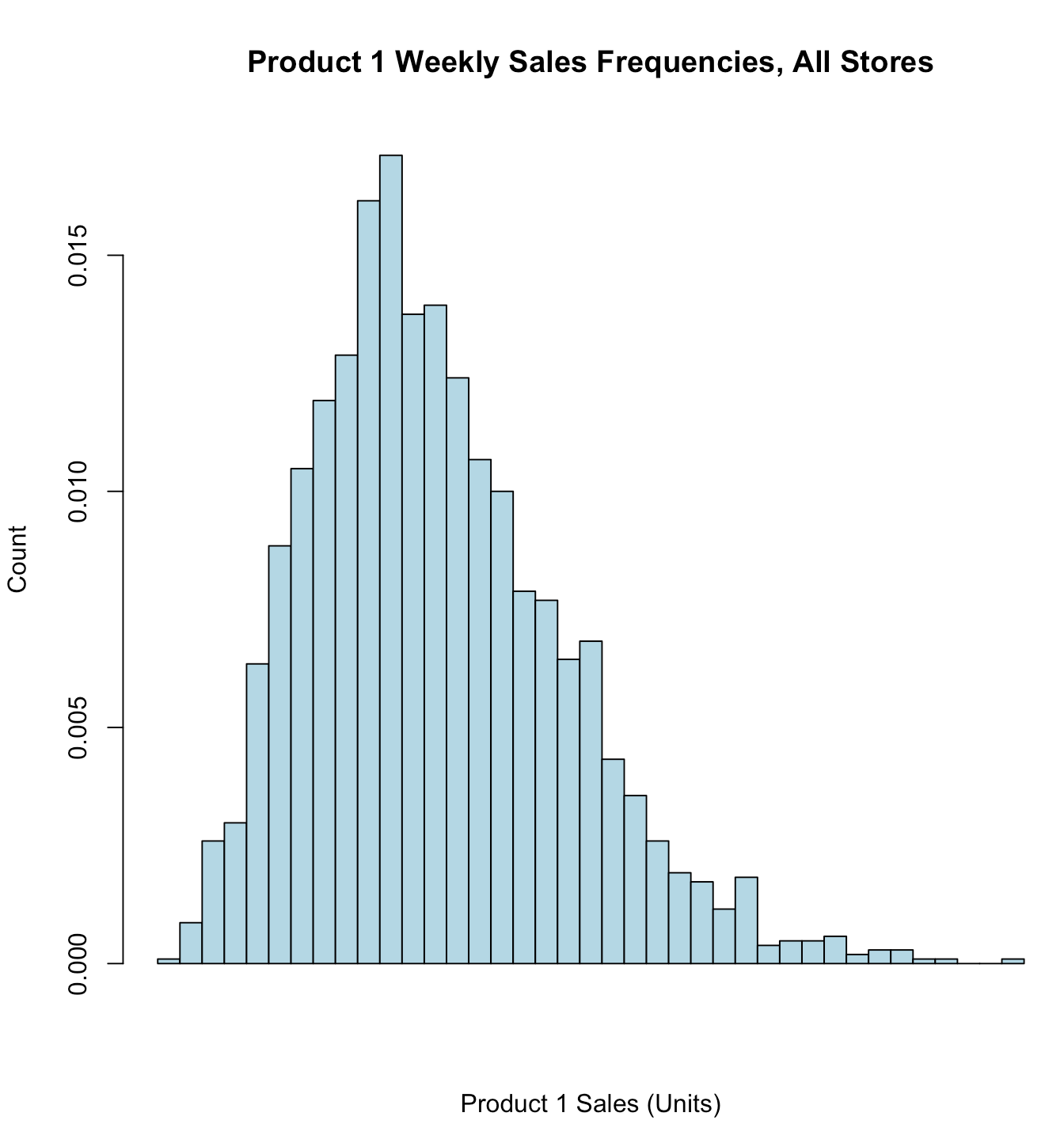
# 添加标题、x轴y轴说明 hist(store.df$p1sales, main = "Product 1 Weekly Sales Frequencies, All Stores", xlab = "Product 1 Sales (Units)", ylab = "Count")
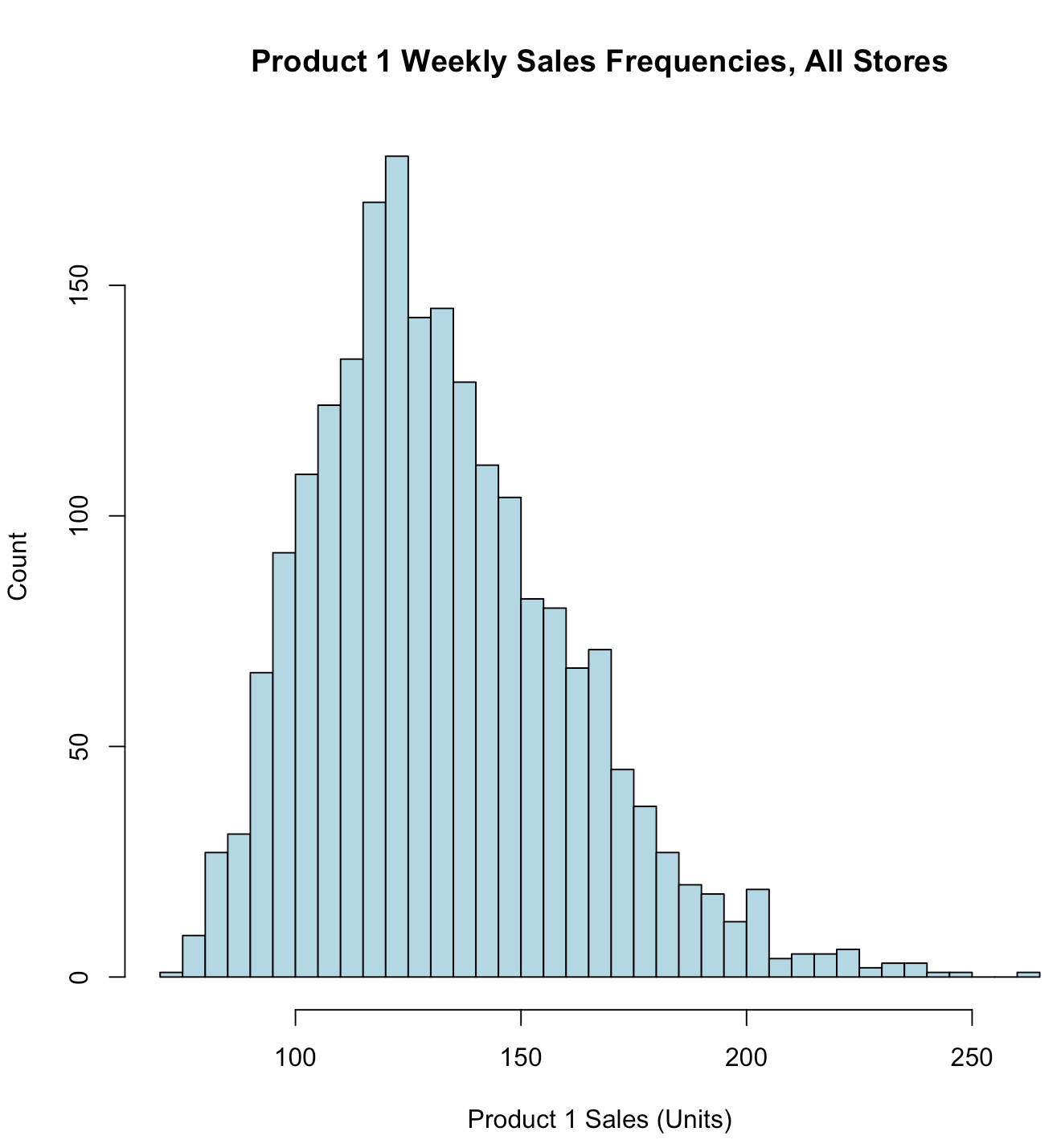
hist(store.df$p1sales, main = "Product 1 Weekly Sales Frequencies, All Stores", xlab = "Product 1 Sales (Units)", ylab = "Count", breaks = 30, # more columns col = "lightblue" # colore the bars )
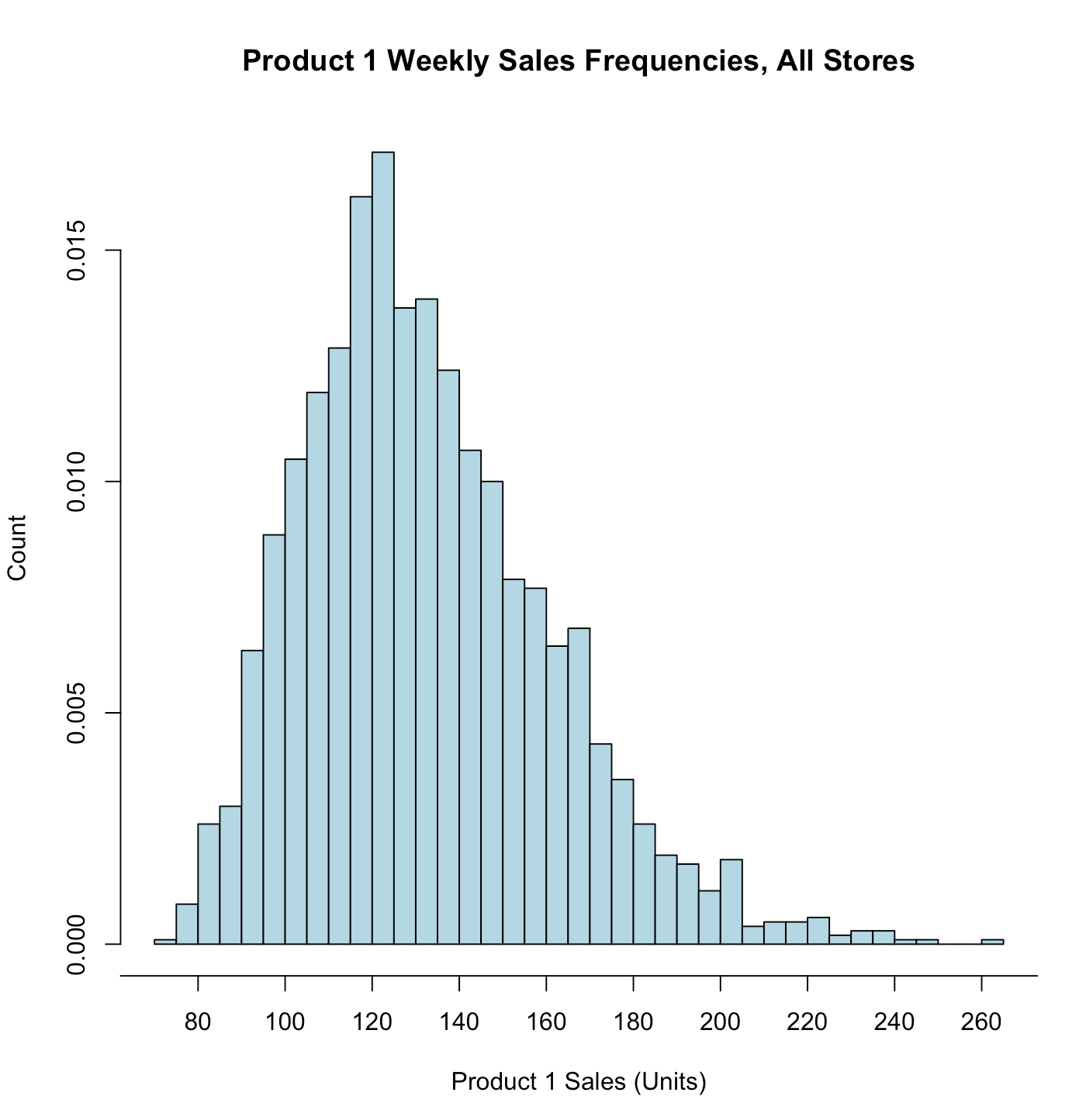
hist(store.df$p1sales, main = "Product 1 Weekly Sales Frequencies, All Stores", xlab = "Product 1 Sales (Units)", ylab = "Count", breaks = 30, col = "lightblue", freq = FALSE, # means plot density, not counts xaxt="n" # means x-axis tick mark is set to "none" )
freq
freq 参数用于控制直方图的纵轴显示的是频数(counts)还是密度(density)。当 freq 设置为 TRUE 时,默认值,纵轴显示的是频数,即每个分箱内数据的数量;当 freq 设置为 FALSE 时,纵轴显示的是密度,即每个分箱内数据的概率密度。
概率密度是概率论中用于描述连续随机变量的概率分布的概念。它在数学上是一个非负实值函数,通常用于描述某个随机变量落在某个区间内的概率。
对于一个连续随机变量,它可能取无穷多个可能的取值,因此我们不能像离散随机变量那样直接计算某个特定值的概率。相反,我们通常关注某个区间内的概率,这个区间越小,计算的概率越准确。概率密度函数(Probability Density Function,PDF)就是用来描述随机变量在某个区间内的概率密度的函数。
在数学上,对于一个连续随机变量 X,其概率密度函数 f(x) 满足以下两个性质:
非负性:对于所有的 x,有 f(x) ≥ 0。
总面积为1:整个定义域内的概率密度函数的积分等于1,即 ∫f(x)dx = 1。
概率密度和频数之间的关系涉及到连续随机变量和离散随机变量的概率分布。下面分别讨论它们的关系: 1. 连续随机变量的概率密度和频数的关系: 对于连续随机变量,概率密度函数(PDF)描述了随机变量落在某个区间内的概率密度,而不是具体的概率值。概率密度函数在某个区间上的值越大,表示该区间内的数据更加密集,概率密度更高。 直方图是用于表示连续随机变量的分布的一种常用方法。在直方图中,将数据分成多个等宽的分箱,并统计每个分箱内数据的频数,然后通过归一化处理,得到每个分箱内的频率(即频数除以样本总数),从而得到一个近似的概率密度分布。 2. 离散随机变量的概率密度和频数的关系: 对于离散随机变量,概率质量函数(PMF)描述了随机变量取某个特定值的概率。每个可能的取值都有一个概率。 直方图同样可以用于表示离散随机变量的分布。在直方图中,每个柱子代表了随机变量取某个特定值的频数,频数表示了该值在样本中出现的次数。由于离散随机变量的取值是有限的,因此直方图中的柱子通常对应于每个可能的取值,每个柱子的高度表示了该值的频率。 总的来说,概率密度和频数都是用于描述随机变量的分布情况的概念,但在连续随机变量和离散随机变量的情境下有所不同。在连续情况下,我们使用概率密度函数描述概率分布,而在离散情况下,我们使用概率质量函数或频数来描述分布。
归一化
归一化是一种数学或统计方法,用于将数据转换为统一的尺度或范围,以便进行比较、分析或处理。在不同的领域中,归一化可能具有不同的含义和方法,但其基本目标是将数据转换为标准形式,消除尺度差异或使数据具有特定的性质。
在统计学和机器学习中,归一化通常指的是将数据按照一定规则进行缩放,使其落入特定的范围或分布。这有助于提高模型的稳定性和收敛速度,以及降低不同特征之间的影响。
常见的归一化方法包括:
最小-最大缩放(Min-Max Scaling) :将数据线性缩放到指定的范围(通常是 [0, 1]),公式为:
Z-Score 标准化(Z-Score Normalization) :也称为标准化,将数据转换为均值为 0、标准差为 1 的正态分布,公式为:
$$
x_{\text{norm}} = \frac{x - \mu}{\sigma}
$$
小数定标标准化(Decimal Scaling) :将数据除以一个适当的基数(例如 10 的幂),使得数据的绝对值最大不超过 1。
归一化可以确保数据在不同特征之间具有可比性,并且有助于提高模型的性能和稳定性。
axis()
# side=1 x轴; side=2 y轴; at=sqp() 修改间隔 axis(side = 1, at=seq(60, 300, by=20)) # add "60", "80", ...
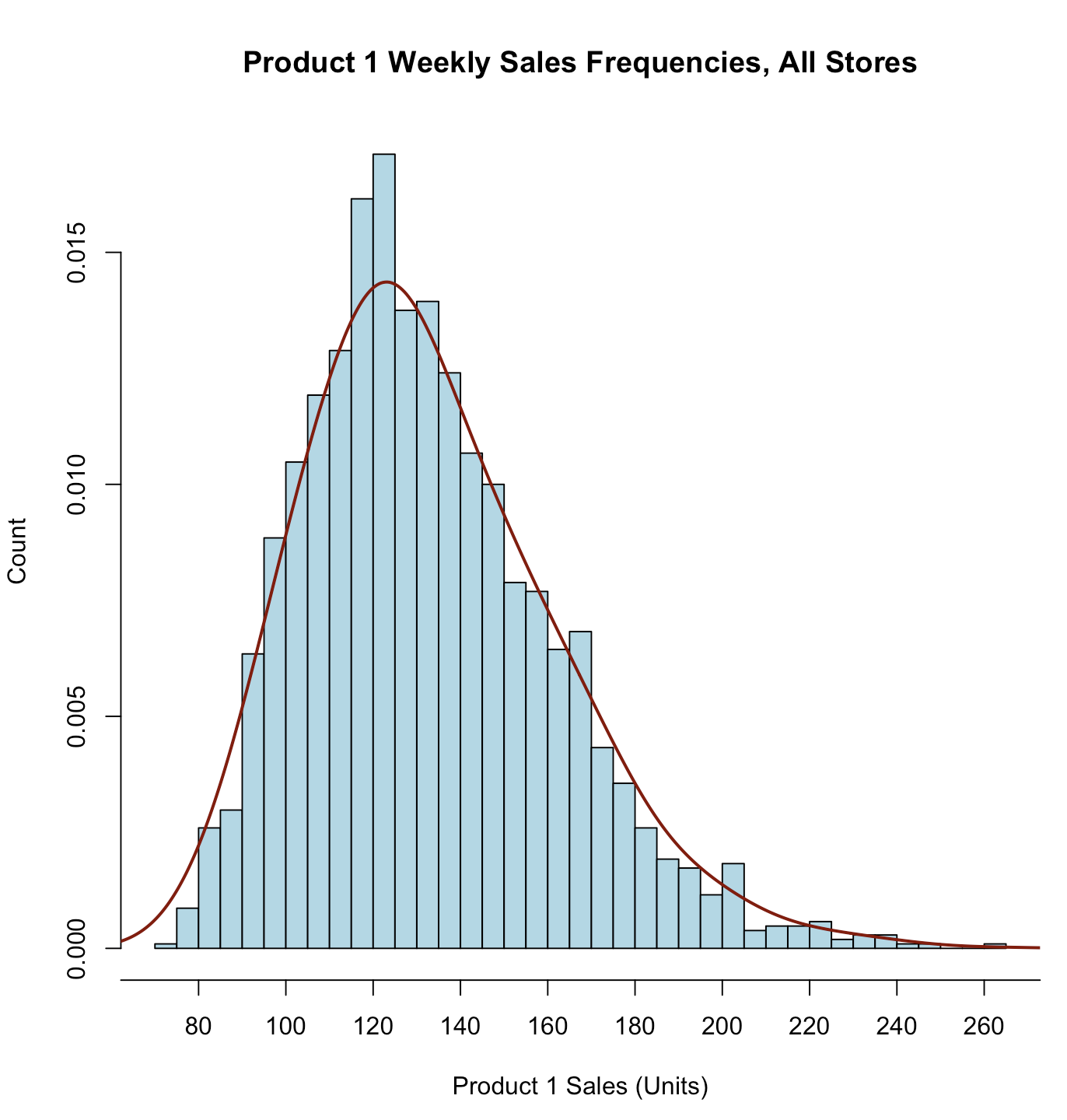
lines()
lines(density(store.df$p1sales, bw=10), # "bw=..." adjusts the smoothing type="l", col = "darkred", lwd=2) # lwd=line width
这是对 density 函数的调用,用于创建概率密度估计图(Kernel Density Estimation,KDE)。以下是其中的各个参数的解释:
density(store.df$p1sales, bw=10):这部分调用了 density 函数,对 store.df$p1sales 列进行概率密度估计。bw=10 指定了带宽参数,控制了估计的平滑程度。带宽越大,估计的曲线越平滑,带宽越小,曲线越精细。这里的 bw=10 表示带宽为 10。
type="l":这个参数指定了要绘制的图形类型。"l" 表示绘制一条折线图。折线图将估计的密度曲线作为折线绘制。
col="darkred":这个参数指定了绘制的折线的颜色。"darkred" 表示深红色。
lwd=2:这个参数指定了绘制的折线的线宽。lwd=2 表示线宽为 2 像素。
type
type 参数用于指定绘图的类型,除了 “l”(折线图)之外,常用的取值还有:
“p”:绘制散点图,即仅绘制数据点而不连接它们。
“b”:绘制数据点并将它们连接成线段,从而形成折线图。与 “l” 类似,但是在每个数据点处绘制一个大点。
“o”:与 “b” 类似,但在每个数据点处绘制一个小圆圈,而不是大点。
“h”:绘制直方图,即垂直的线条用于表示频率。
“s”:绘制阶梯图,即通过垂直和水平线段连接每个数据点,从而形成阶梯状的图形。
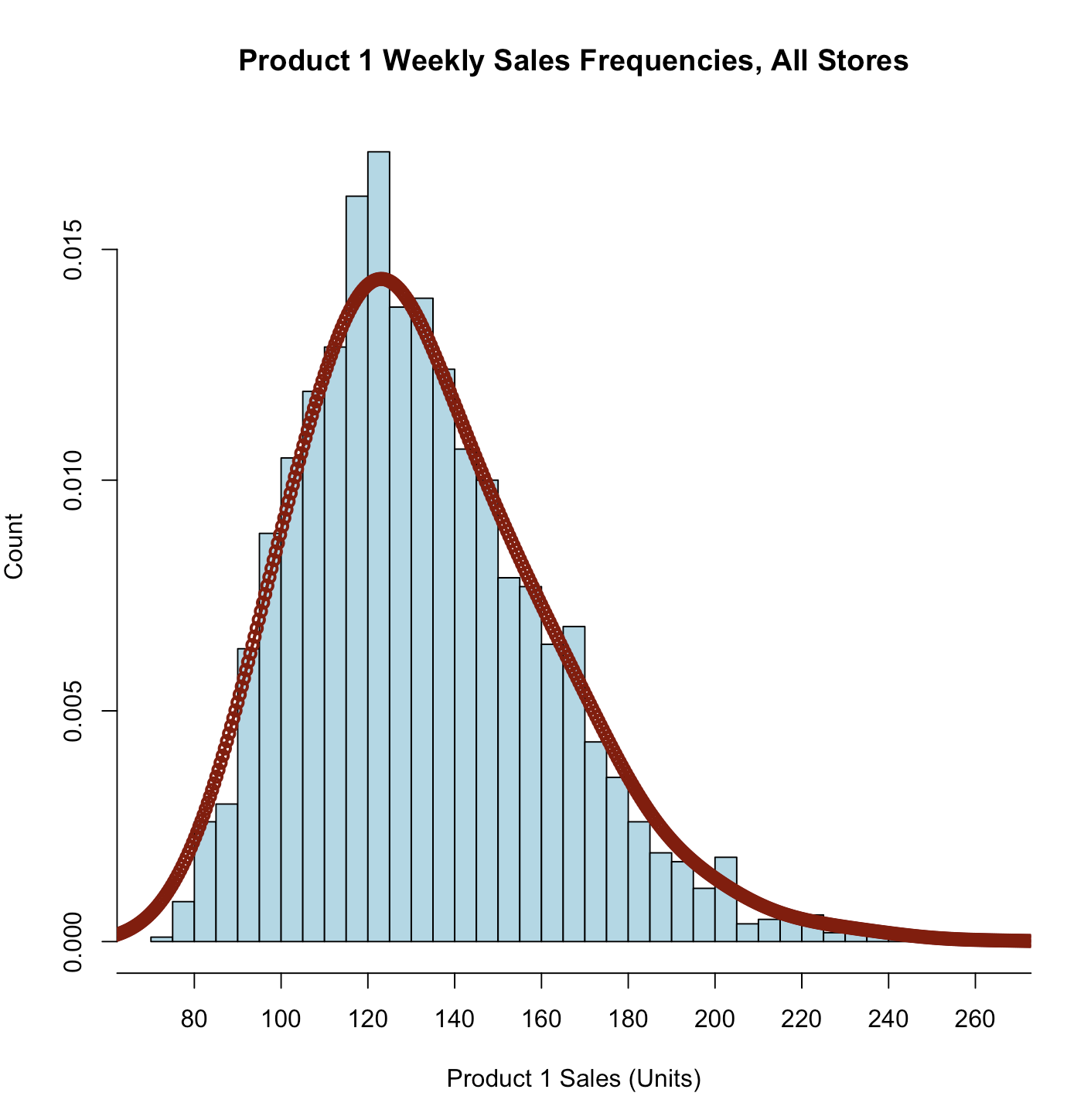
lines(density(store.df$p1sales, bw=10), # "bw=..." adjusts the smoothing type="o", col = "darkred", lwd=2) # lwd=line width
二、week1 code
# install.packages ("readxl") # install.packages ("psych") # install.packages ("car") # install.packages ("gpairs") # install.packages ("grid") # install.packages ("lattice") # install.packages ("corrplot") # install.packages ("gplots") library("readxl") library("psych") library("car") library("gpairs") library("grid") library("lattice") library("corrplot") library("gplots") # 获取当前已加载文件的目录 file_dir <- dirname(parent.frame(2)$ofile) print(file_dir) # 将工作目录设置为当前已加载文件的目录 setwd(file_dir) store.df <- read.csv("Data_Descriptive.csv", stringsAsFactors=TRUE) str(store.df) table(store.df$p1price) p1.table <- table(store.df$p1price) p1.table str(p1.table) plot(p1.table) table(store.df$p1price, store.df$p1prom) p1.table2 <- table(store.df$p1price, store.df$p1prom) p1.table2[ ,2] / (p1.table2[ ,1] + p1.table2[ ,2]) plot(p1.table2) min(store.df$p1sales) max(store.df$p1sales) mean(store.df$p1prom) median(store.df$p2sales) var(store.df$p1sales) sd(store.df$p1sales) IQR(store.df$p1sales) mad(store.df$p1sales) quantile(store.df$p1sales, probs = c(0.25, 0.5, 0.75)) quantile(store.df$p1sales, probs = c(0.05, 0.95)) # central 90% data quantile(store.df$p1sales, probs = 0:10/10) quantile(store.df$p1sales, probs = seq(from=0, to=1, by=0.1)) mysummary.df <- data.frame(matrix(NA, nrow=2, ncol=2)) # 2 by 2 empty matrix names(mysummary.df) <- c("Median Sales", "IQR") # name columns rownames(mysummary.df) <- c("Product 1", "Product 2") # name rows mysummary.df["Product 1", "Median Sales"] <- median(store.df$p1sales) mysummary.df["Product 2", "Median Sales"] <- median(store.df$p2sales) mysummary.df["Product 1", "IQR"] <- IQR(store.df$p1sales) mysummary.df["Product 2", "IQR"] <- IQR(store.df$p2sales) mysummary.df summary(store.df) summary(store.df$Year) summary(store.df, digits = 2) # 保留小数点后两位 library(psych) # install if needed describe(store.df) describe(store.df[,c(2, 4:9)]) dim(store.df) head(store.df) tail(store.df) some(store.df) str(store.df) summary(store.df) describe(store.df) apply(store.df[ 2:9], MARGIN = 2, FUN = mean) apply(store.df[ , 2:9], 2, sum) apply(store.df[ , 2:9], 2, sd) hist(store.df$p1sales) # 添加标题、x轴y轴说明 hist(store.df$p1sales, main = "Product 1 Weekly Sales Frequencies, All Stores", xlab = "Product 1 Sales (Units)", ylab = "Count") colors() hist(store.df$p1sales, main = "Product 1 Weekly Sales Frequencies, All Stores", xlab = "Product 1 Sales (Units)", ylab = "Count", breaks = 30, # more columns col = "lightblue" # colore the bars ) hist(store.df$p1sales, main = "Product 1 Weekly Sales Frequencies, All Stores", xlab = "Product 1 Sales (Units)", ylab = "Count", breaks = 30, col = "lightblue", freq = FALSE, # means plot density, not counts xaxt="n" # means x-axis tick mark is set to "none" ) hist(store.df$p1sales, main = "Product 1 Weekly Sales Frequencies, All Stores", xlab = "Product 1 Sales (Units)", ylab = "Count", breaks = 30, col = "lightblue", freq = FALSE, # means plot density, not counts xaxt="n" # means x-axis tick mark is set to "none" ) # side=1 x轴; side=2 y轴; at=sqp() 修改间隔 axis(side = 1, at=seq(60, 300, by=20)) # add "60", "80", ... lines(density(store.df$p1sales, bw=10), # "bw=..." adjusts the smoothing type="l", col = "darkred", lwd=2) # lwd=line width lines(density(store.df$p1sales, bw=10), # "bw=..." adjusts the smoothing type="o", col = "darkred", lwd=2) # lwd=line width