Q：处理器、进程或者节点各自独立，如何才能够达成共识？

一般情况下，节点间可以彼此传递消息达成一致。但是有故障节点存在的是时候，故障节点可能会向其他节点发送一个错误值，或者发送一些随即值，甚至不发送，导致每个处理器获取到不同的数据，最终计算出不一致的结果。

比如，处理器间的时钟同步，集群服务器间的数据同步

Reaching Agreement in the Presence of Faults 论文作者提出一种方法来消除错误处理器的影响 - 通过使用循环多轮的信息交换方案来处理;这样的方案可能会迫使有错误的处理器暴露自己有错误，或者至少使其行为与没有错误的处理器保持一致，从而使后者能够达成一致(当然，是在一定的条件下)。

Assumptions

假设总共有n个独立节点，其中错误节点m个，并且不知道具体是哪些节点出现了问题。节点之间只能双方彼此通信，并且假设数据传输是有保障的并且无延迟。接收方可以识别消息的发出者。
每个节点n具有私有值Vn（可以理解为当前该节点的状态，比如负载等）。对于给定的m、n，通过彼此间的信息交换，让每个节点持有一个所有节点私有值的向量。最终达成：

• 非故障节点能够计算得到完全相同的向量;
• 该向量中，非错误节点的所对应的元素元素，是该节点的私有值

举个例子：

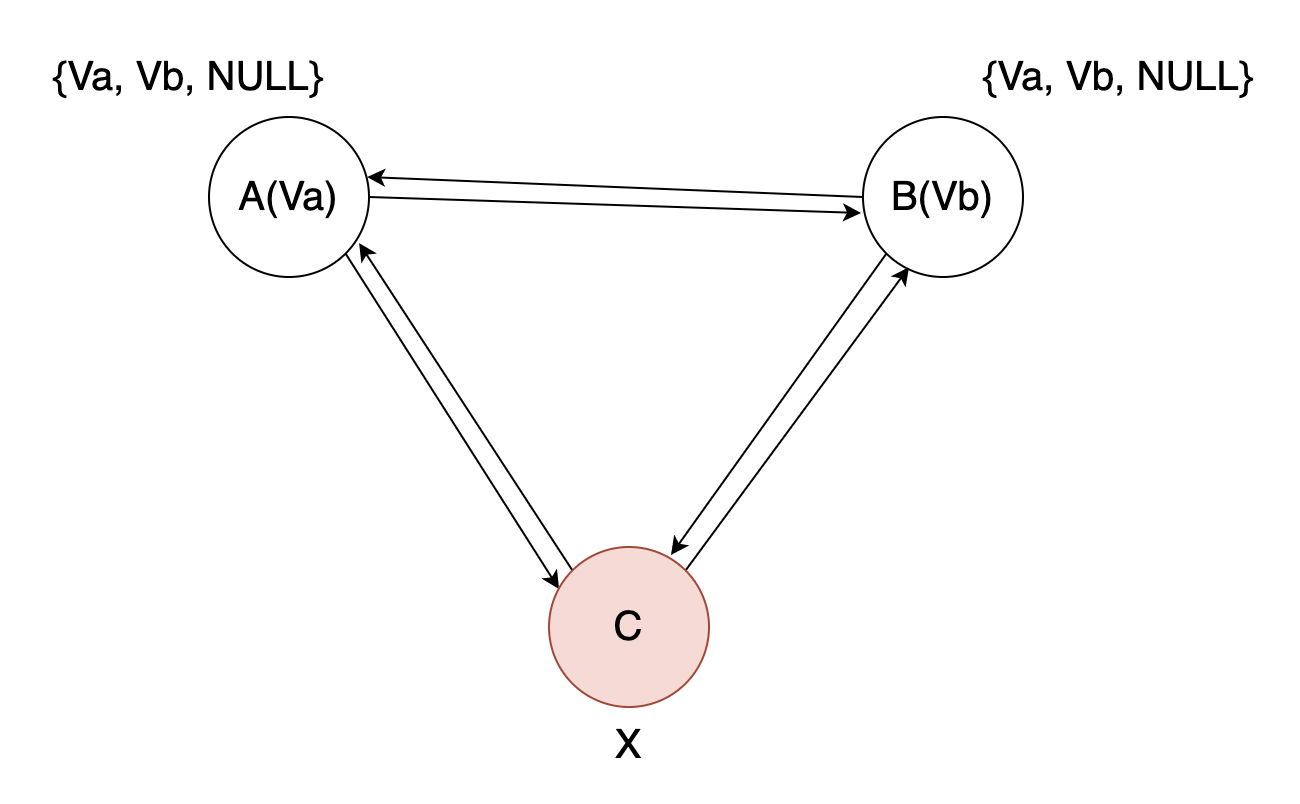
交互一致性

虽然我们不需要最终知道哪些节点是有问题的，与错误节点对应的向量元素也可以是任意的;但是正确节点对于错误节点的向量元素必须是一致的。

比如下面的这种情况是不被接受的：

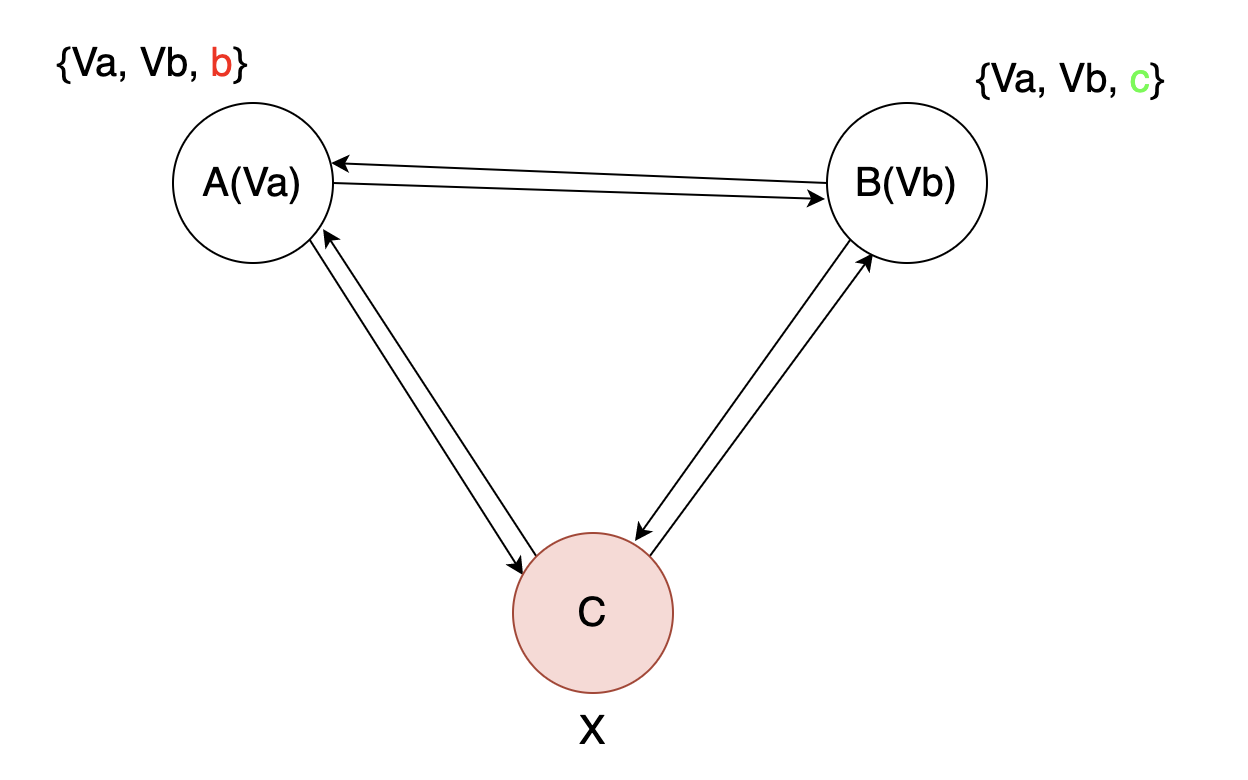
正确节点对所有节点(包括有故障的节点)持有的值达成共识，最终得到（交互式）一致性向量。这样，每个节点就能够通过对该向量的计算，继续得到业务上的所需要的值。

单节点错误

n=4, m=1

首先可以假设 n=4, m=1。进行两轮信息交换：

1. 各个节点先把自己的私有值发给其他节点
2. 各个节点彼此交换第一轮收到的信息

在信息交换过程中，错误节点可能会发出错误的值，或者不发出任何值，来干扰其他正常节点的计算。对于一个正常节点，如果没有收到节点N的消息，会将其置为默认值（假设为NULL）。

STEP1:

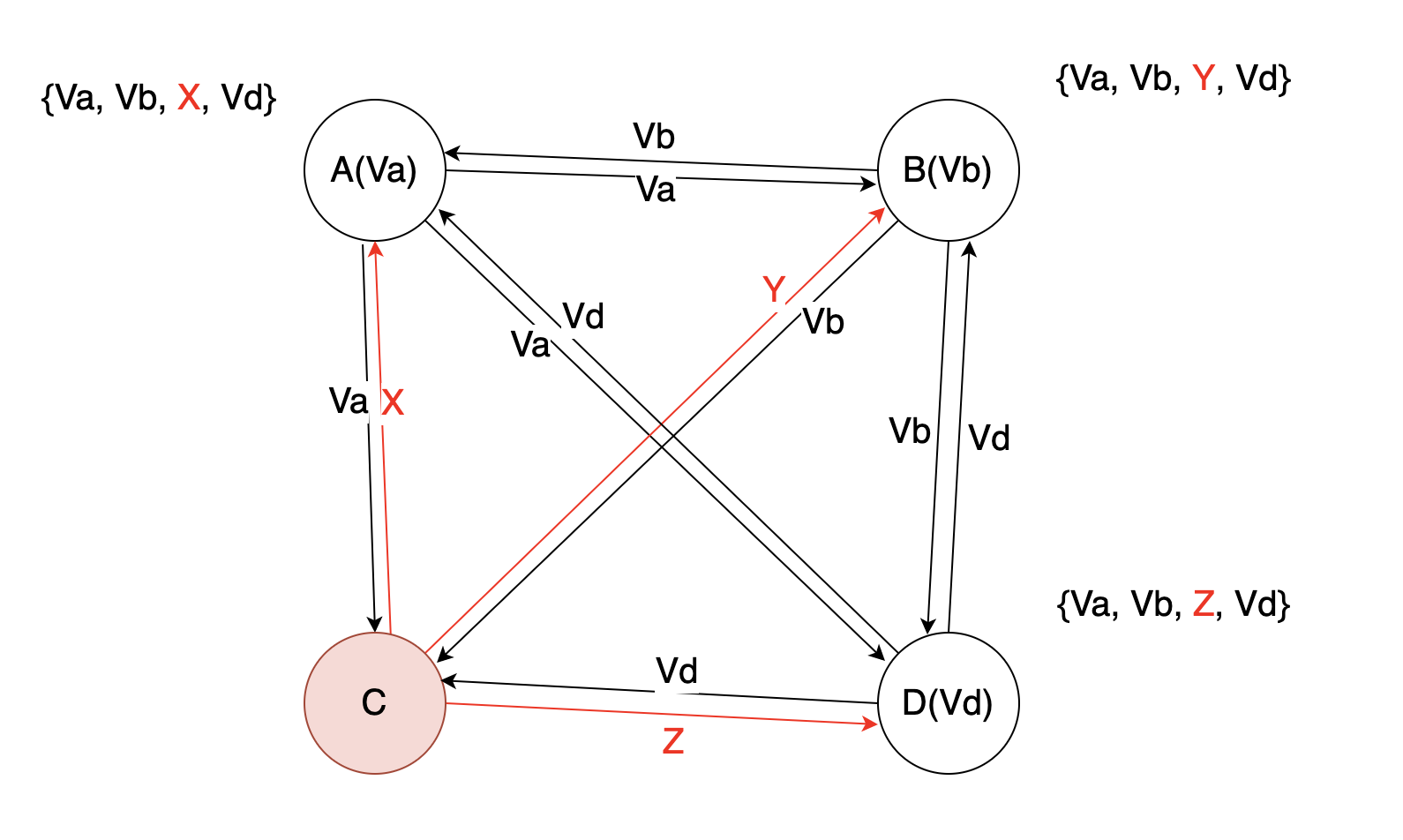
STEP2:

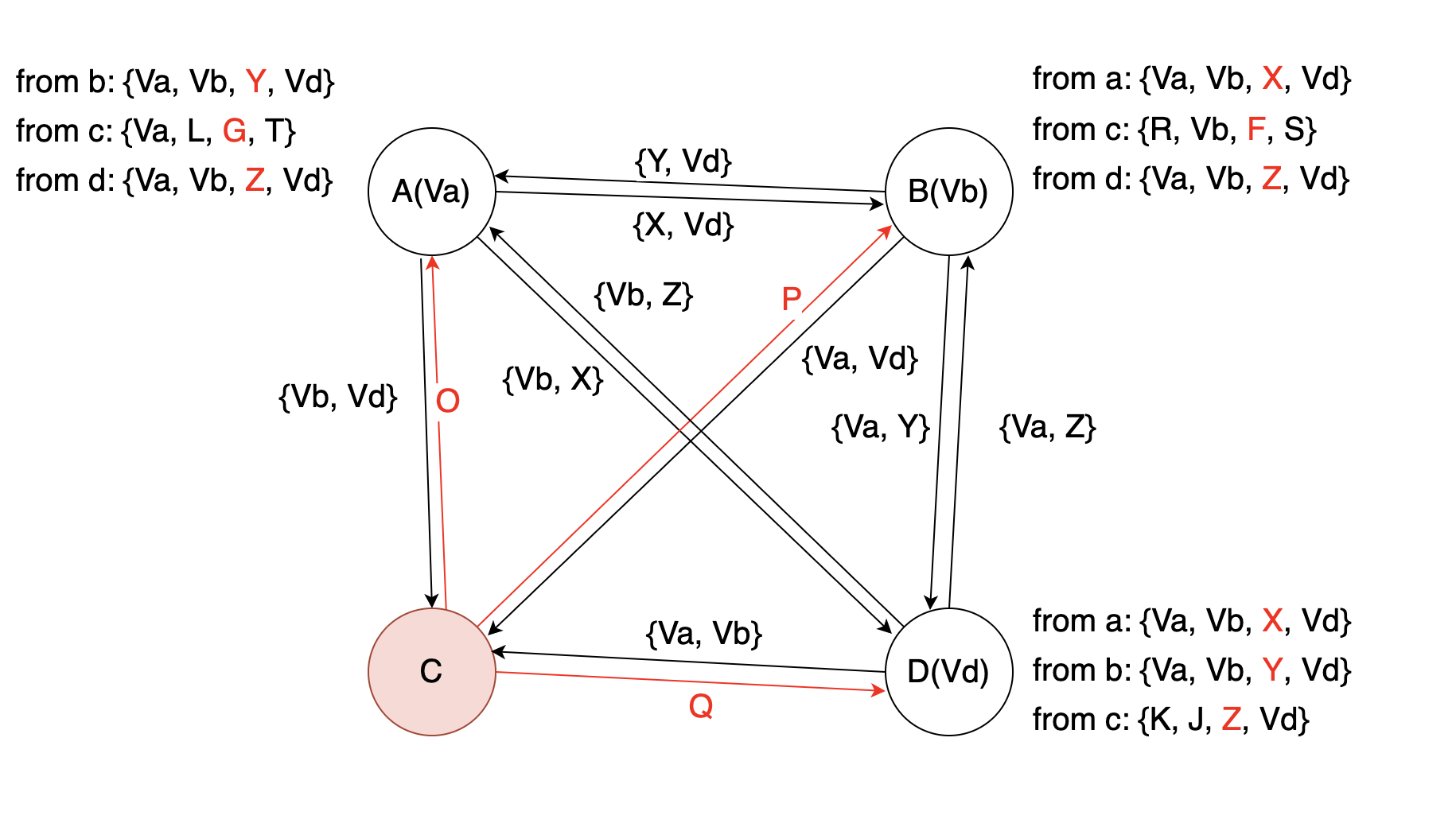
在两轮信息交换完成后，每个节点都会持有“一组”向量值元素。节点可以选取“多数”作为认可的元素值，形成最终的向量。

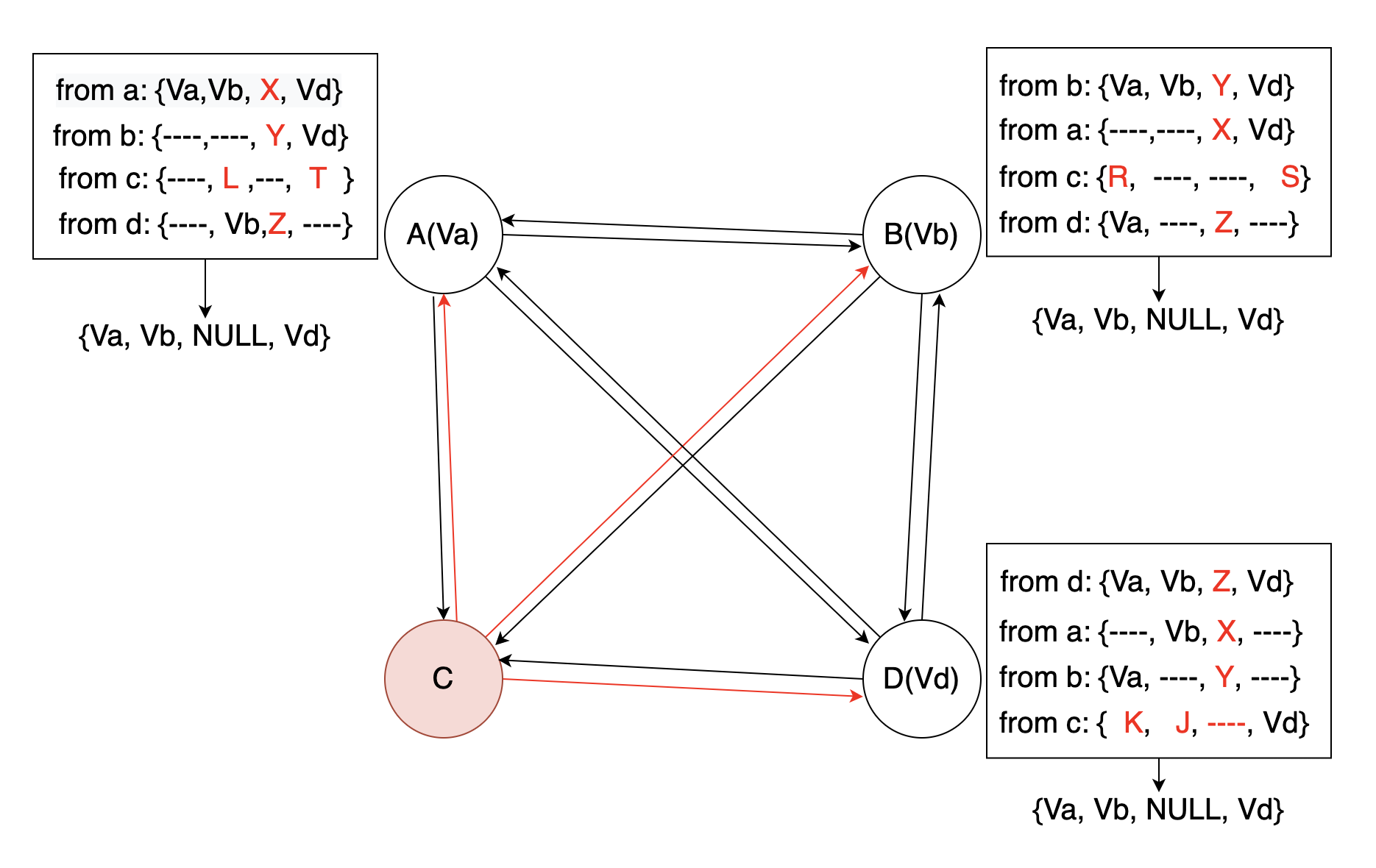
多节点错误

仅仅两轮信息交换不足以达成共识：

STEP1:

STEP2:

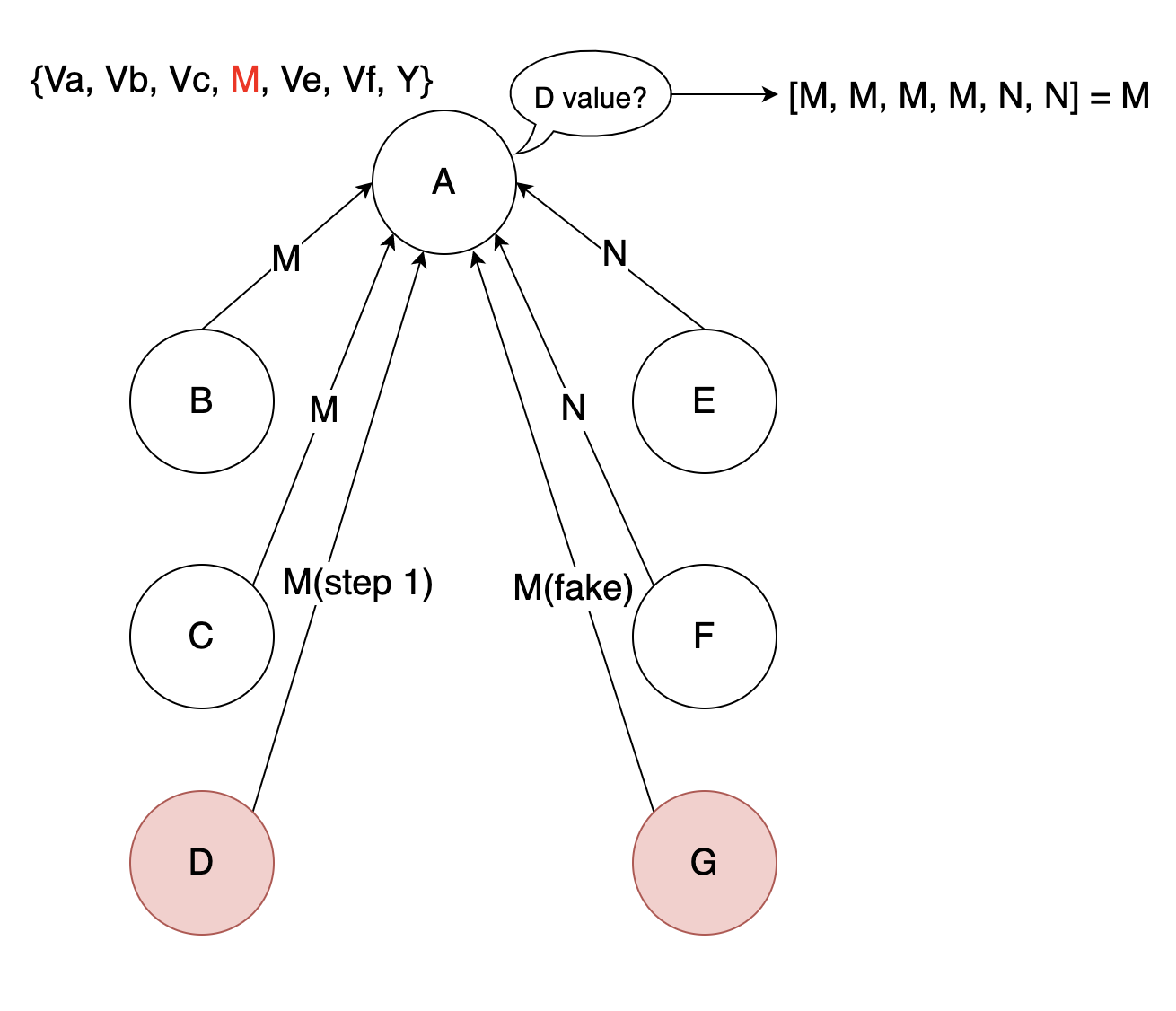
Finally:

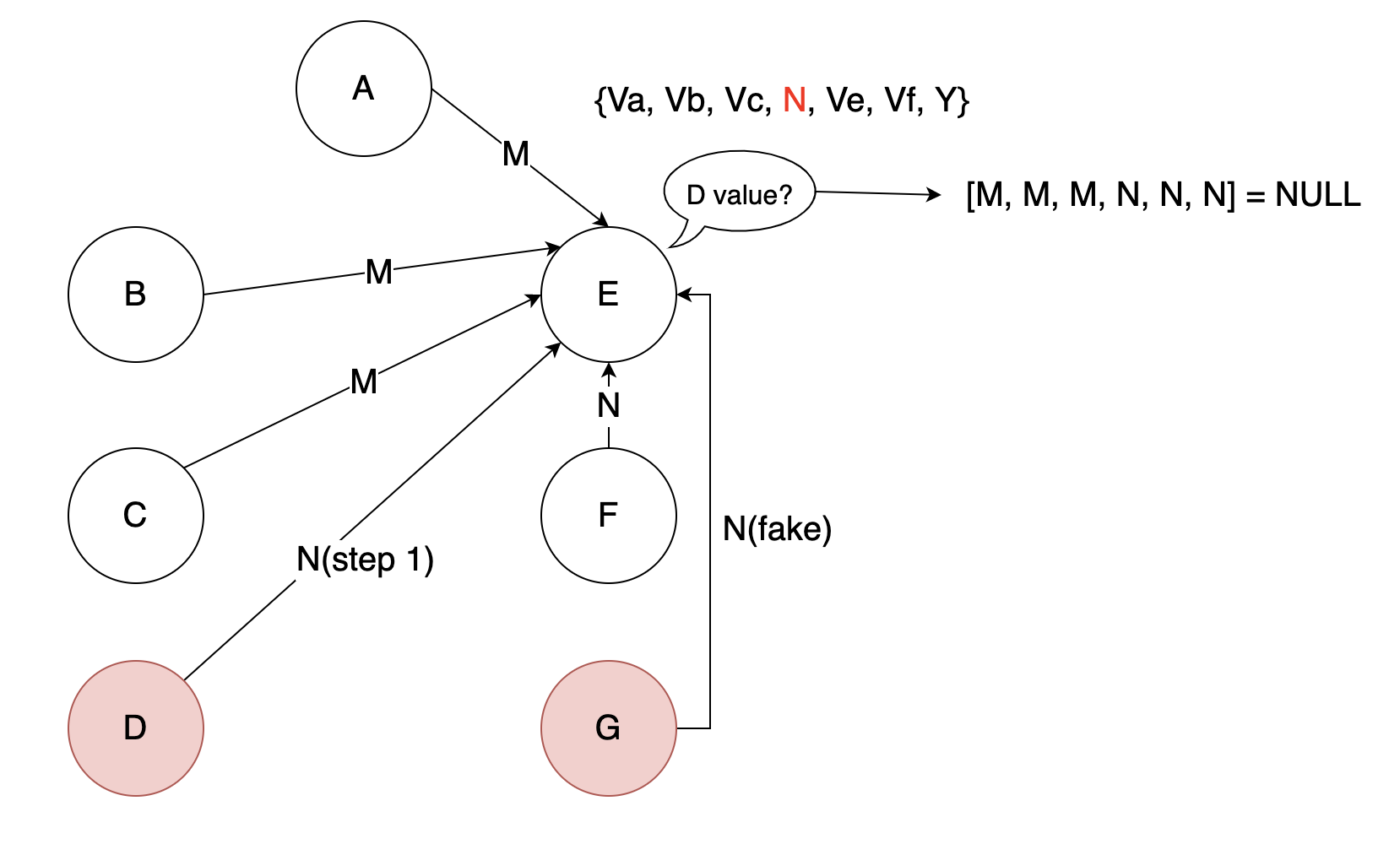
继续下一轮交换信息…

m+1 轮后：

P: 节点集合 V: 值的集合

定义：
1）w=p1p2p3…pr, σ(w) 意为 pr -> p(r-1) -> p(r-2) -> ··· -> p2 -> p1，Vpr最终流转到p1的结果。
2）对于一个单节点，σ§ = Vp
3）如果一个节点q是正常的，那么他一定满足：对于任意的集合组成的字串w和任意节点p，

σ(pqw) = σ(qw) 同理如果一个集合全部是正常节点，那么集合所组成的字串 w=p1p2p3...pr，和一个任意节点p', 一定能够满足 σ(pwp') = σ(wp')

那么，通过如下方法帮助p节点得到q值（总节点n，错误节点m，n>=3m+1）：

1. 对于集合P的某个大小超过(n+m)/2的子集Q，σp(pwq) = v 对于每个长度不大于m的字串w（取自Q）都成立，那么p记录下v；
2. 否则，算法将递归应用m-1，n-1，使P-{q}来替代P，并且对于每个长度不大于m的字串w（取自于P-{q}）

σp'(pw) = σp(pwq) 如果在这向量n-1个元素里有至少(n+m)/2个元素值相同，p记录下该值，否则记录NIL值。

step1：（目的是确定源节点q正确与否）一定能够找到一个全部是正常节点的集合Q(size <= m)，使得正常的源节点q的值，经过Q处理后，依然不变。

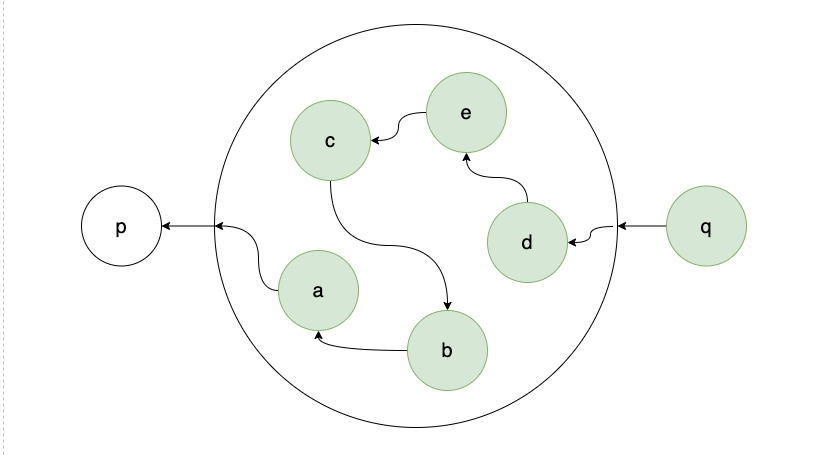
step2：（目的是对错误节点的值达成共识）如果源节点q没能满足step1，说明q在乱发值，q是一个问题节点。

q向d发送X：

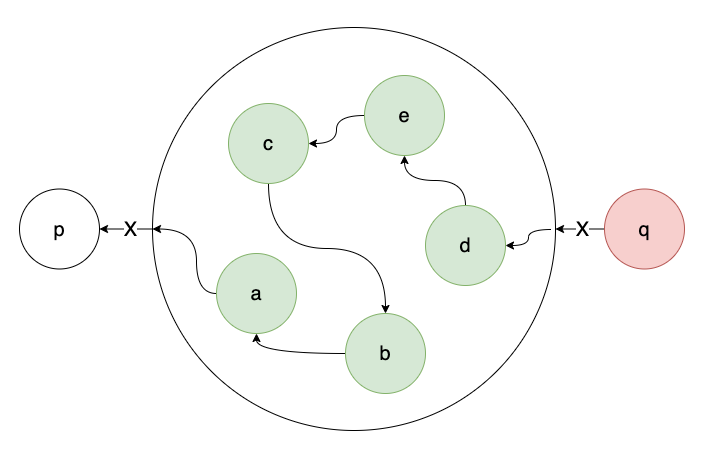
q向e发送Y：

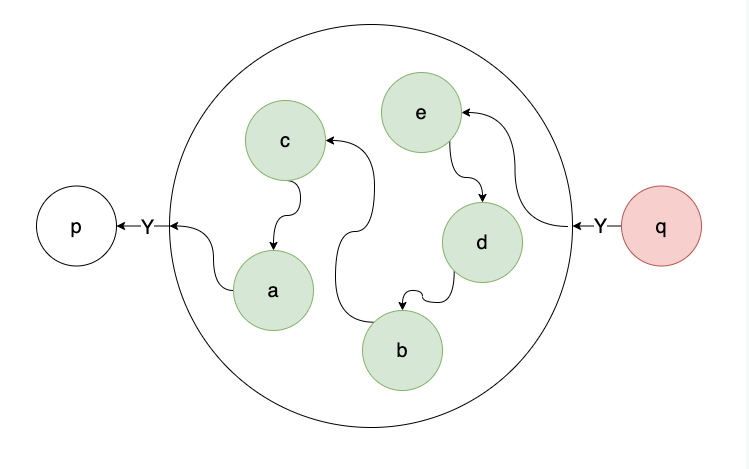
所以q的值是多少不重要了，重要的是其他节点要对q的值达成共识。做法，把问题节点q踢出去，询问其他节点，在他们眼里，q是多少。如果某个值Vq’超过半数认可，那么就以Vq’作为q的值，否则，记默认值NIL。即：

σp'(pw) = σp'(pwq') = σp(pwq'q) = σp(pwq)

p 问q’（中间也经过了step1的处理），你眼里q是多少？如果获得了不一致的答案，说明q’也有问题，踢了，再问其他节点，最终得到一个正常节点认可的值Vq’1
最终，p得到了其他所有正常节点眼里的q值: Vq’1 Vq’2 … Vq’k，如果在这中间，某个值Vq’m超过了半数，那么以Vq’m作为q的值，否值取默认值NIL。
这个过程就像是询问“认可值”，只要获得了足够多的“认可”，就可视Vq为q的值。

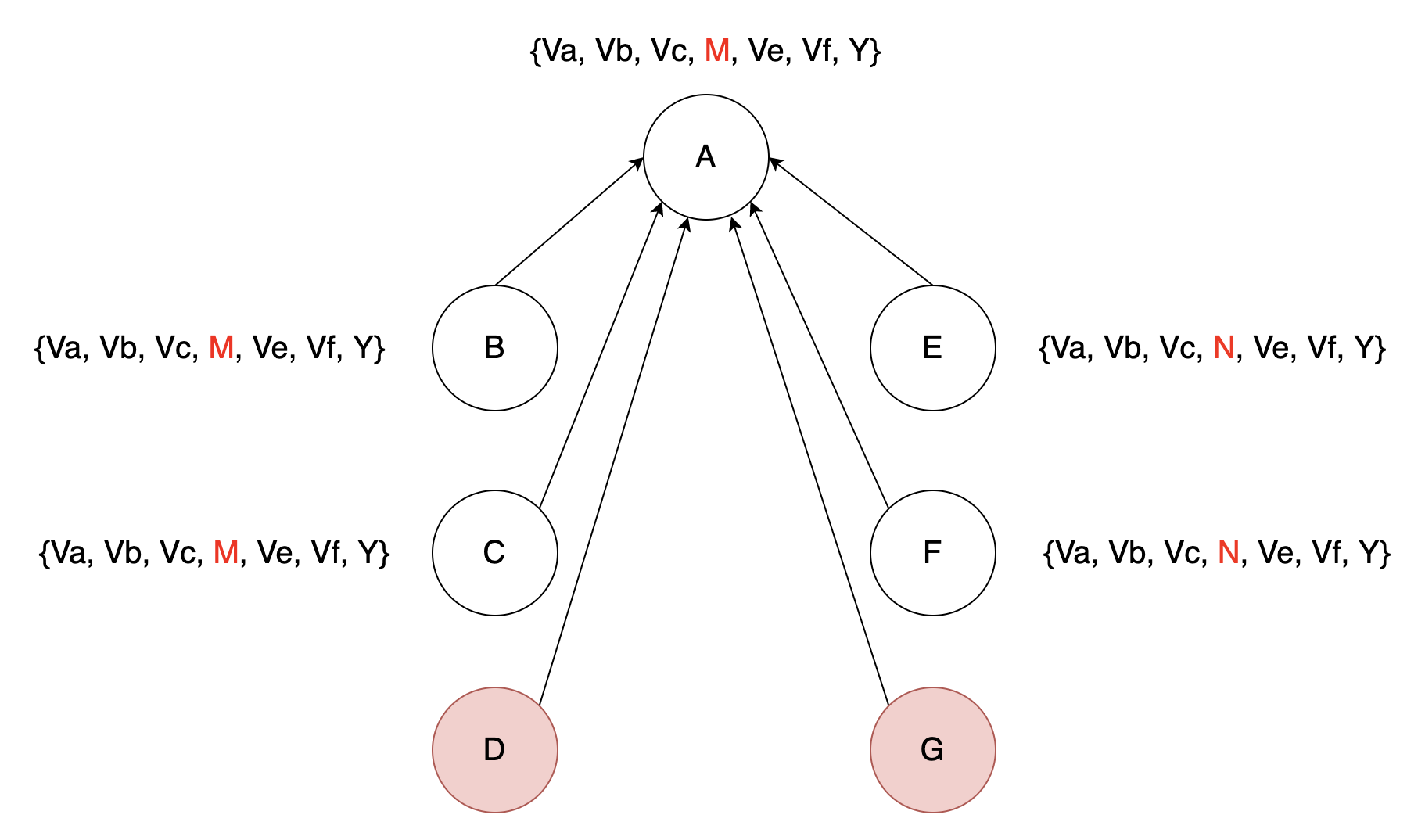
n=7, m=2

以A为主视角

step1: 每个节点把自己的值发送给其他节点

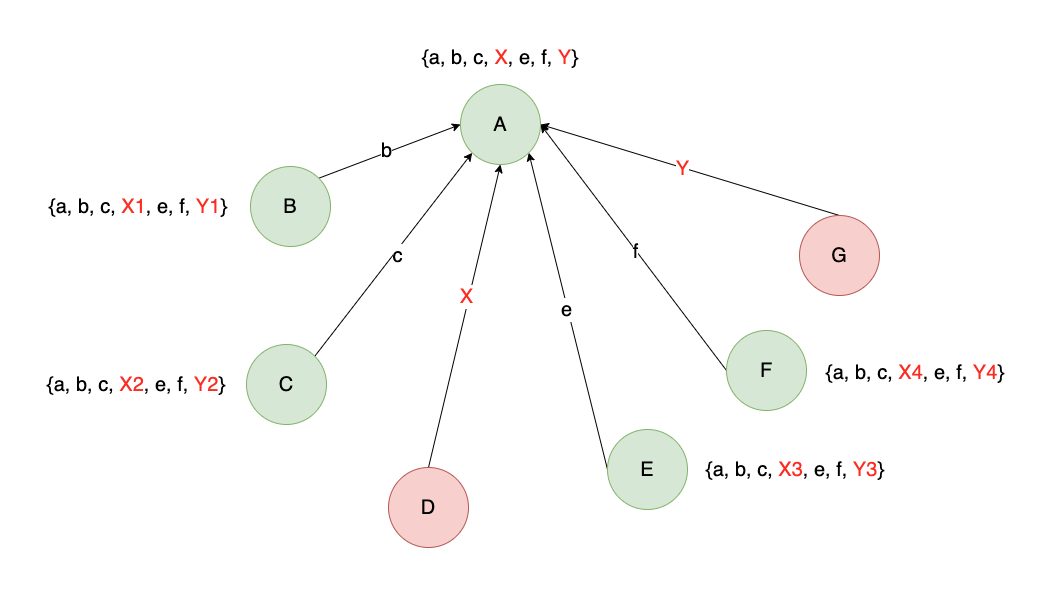
step2: 每个节点分享上一轮接收到的值

step3: 每个节点再次分享上一轮接收到的值

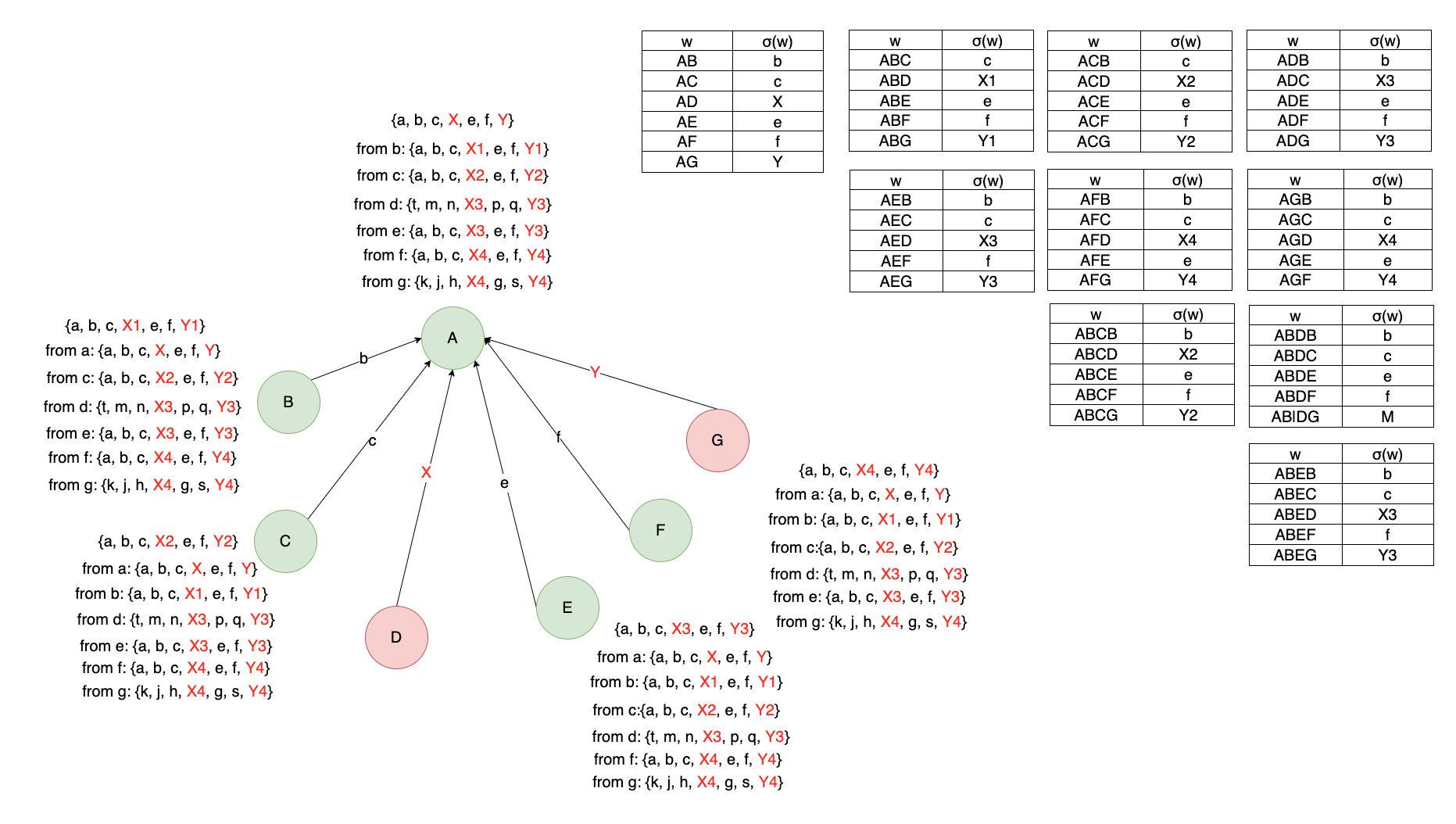
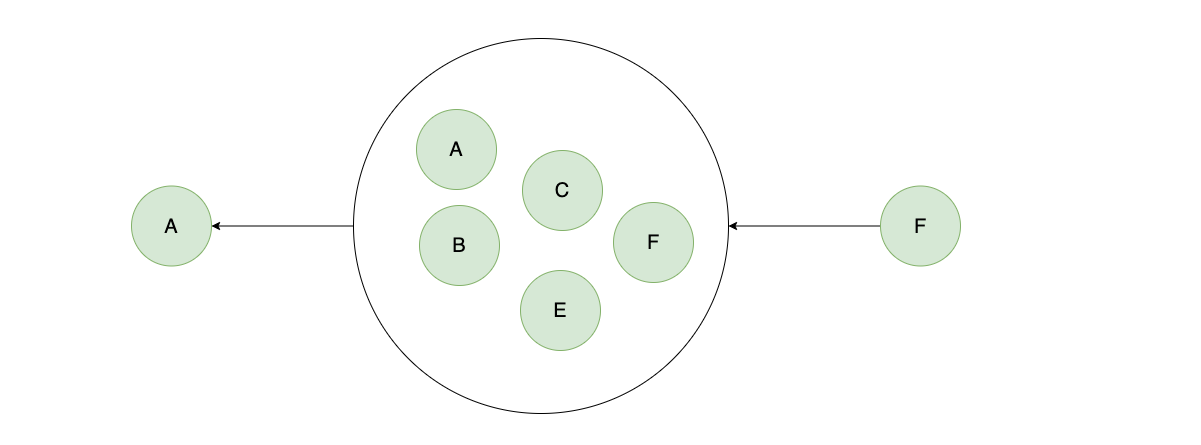
• 对于一个正常节点，经过子集Q，抵达A的值不会变

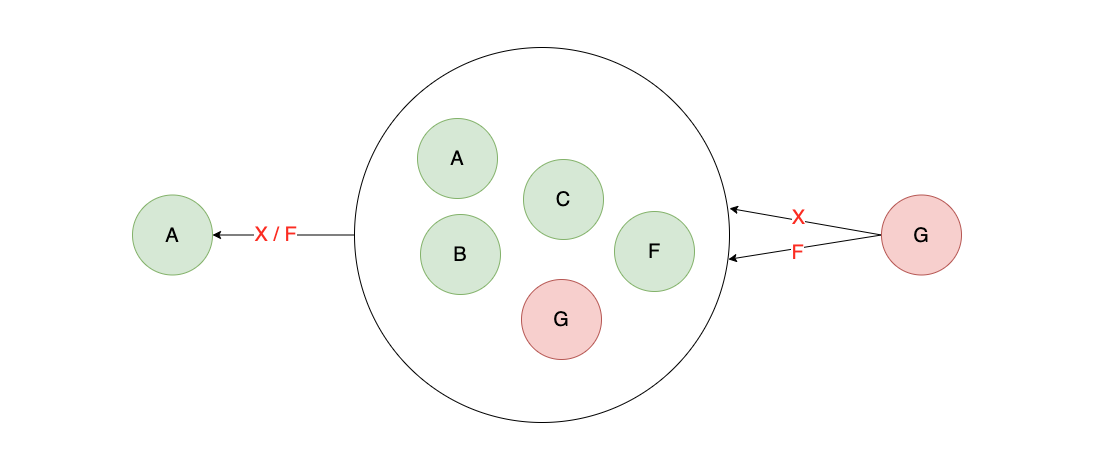
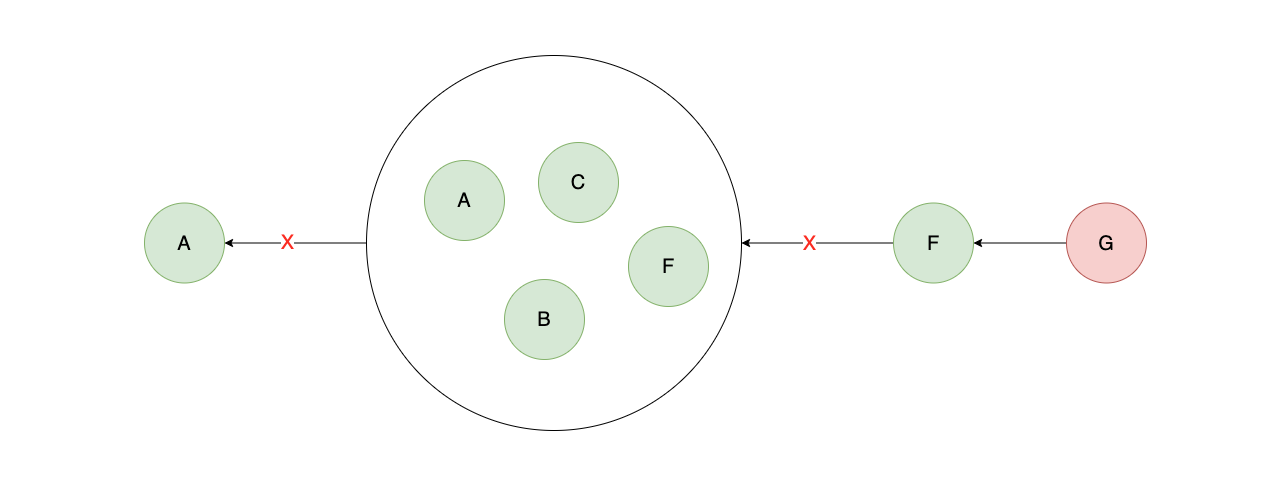
• 对于一个非正常节点，经过子集Q，抵达A的值可能会变。此时需要踢出错误节点，来达成值的一致

---

---

---

拜占庭国王放下手中的 Reaching_agreement_in_the_presence_of_faults.pdf，陷入沉思。

最近他的军队正在攻打敌方同样强大的城池，需要将领们协同一致才可制胜。而他也知道，将军们中间有叛徒，正因此进攻才耽搁许久。忽然他眉头一皱，计上心来！

国王究竟想到了什么办法呢？请看下回：

---

---

---

回想一下，上一节给出的过程需要两轮信息交换，第一轮“我的私有值是”，第二轮“节点x告诉我他的私有值是....”。在m个节点故障的一般情况下，需要m + 1轮通信。为了描述该算法，可以以更通用的方式描述这种消息交换。
  
<center>P: 节点集合</center>  
<center>V: 值的集合</center>  
对于 k>=1. 定义k-scenario为从非空字符串（可能含有重复）P(length <= k+1) 映射到 V。对于一个给出的k-level scenario σ 和字符串 w= p1p2...pr, 2<=r<=k+1, σ(w) 意为 pr-\>p(r-1)-\>p(r-2)->···-\>p2-\>p1, 【pr 的私有值】。对于一个单一元素的字符串p，σp指代p的私有值Vp。一个k-level scenario 总结了k轮信息交换的结果。(请注意，如果一个错误的节点伪造其他节点给它的信息，这就相当于对给它的值造假。)对于一个正常节点子集，只有可能是确定的映射：尤其是，一个正常节点在传递消息时总是诚实的，所以对于一个正常节点q，任意节点p，以及字符串w来说，一个scenario一定满足：（也就是传递到q的字符串会原封不动地传达给p）  
<center>σ(pqw) = σ(qw)</center>   
节点p在scenario σ接收的消息由σp对以p开头的字符串的限制操作给出(这句话好难理解，我感觉是在表达，secnario σ 是给来源字串加了一个p头)。现在我们要描述，对于任意m>=0,n>=3m+1, 计算p的过程。对于一个给定的σp, 其中交互一致性向量的元素对应着每个节点p。计算过程如下：  
   
1. 对于P的某个大小>(n+m)/2的子集Q，σp(pwq) = v 对于每个长度<=m的字串w（取自Q）都成立，那么p记录下v； 
2. 否则，算法将递归应用m-1，n-1，使P-{q}来替代P，并且对于每个长度不大于m的字串w（取自于P-{q}）  
<center>σp'(pw) = σp(pwq)</center>  
如果在这向量n-1个元素里有至少(n+m)/2个元素值相同，p记录下该值，否则记录NIL值。  
σp'反应了m-level σ的子场景，其中q被排除在外，并且在σp'每个节点的私有值是它直接从σ中的q获得的值。  
通过对m进行约简，证明上述算法确实保证了交互一致性:  
Basis m=0。此时没有节点是错误的，算法总是在第一步结束。p记录Vq为q的私有值；  
Induction Step m>0. 如果q是正常节点，对于来自于正常节点集合的，长度不大于m的字串w（包括空串），σp(pwq)=Vq。这个集合包含了n-m个成员，多于(n+m)/2，满足了条件1. 此外，满足这些要求的任何其他集合必然包含一个正常节点, 因为集合数量大于(n+m)/2，而n>=3m+1. 因此也必然得到Vq作为可用值。因此算法在第(1)步终止，p按要求记录Vq为q的私有值。  
现在假设q是错误的。我们必须表明p记录下的q私有值Vq和其他正常节点一致。  
首先考虑这种情况：p和其他节点p'都在step1结束，他们都找到了一个合适的集合Q。由于每个集合都包含有(n+m)/2个成员，并且由于P总共只有n个成员，两个集合必须有超过2((n + m)/2) - n = m个公共成员。因为其中至少有一个必须是正常的节点，所以这两个集合必须产生相同的值v。  
接下来我们假设p'在step1退出了，找到了合适的集合Q以及值v，并且p执行step2.