0-1 背包问题

1. 动态规划问题，最好具备两个前提：

  • 最优化原理

    最优化原理指的最优策略具有这样的性质：不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。简单来说就是一个最优策略的子策略也是必须是最优的，而所有子问题的局部最优解将导致整个问题的全局最优。如果一个问题能满足最优化原理，就称其具有最优子结构性质。

  • 无后效性

    无后效性指的是某状态下决策的收益，只与状态和决策相关，与到达该状态的方式无关。某个阶段的状态一旦确定，则此后过程的演变不再受此前各种状态及决策的影响。换句话说，未来与过去无关，当前状态是此前历史状态的完整总结，此前历史决策只能通过影响当前的状态来影响未来的演变。再换句话说，过去做的选择不会影响现在能做的最优选择，现在能做的最优选择只与当前的状态有关，与经过如何复杂的决策到达该状态的方式无关。

2. 分析

你只有一个容量有限的背包，总容量为c，有n个可待选择的物品，每个物品只有一件，它们都有各自的重量和价值，你需要从中选择合适的组合来使得你背包中的物品总价值最大。
抽象问题，可以描述为：

有一个容量为c的背包，总共有n个物品，每个物品的体积为wi，价值为vi，求该背包能容下的最大价值。（每个物品只取一次）
使用xi来标志第i个物品是否放到背包里，则：

  • x1w1 + x2w2 + x3w3 + … + xnwn <= c
  • Max(x1v1 + x2v2 + x3v3 + … + xnvn) = result

根据上面所说的两个前提，可以得到一个公式：

  • if wi > c, result[i, j] = result[i-1, j]
  • else result[i, j] = max(result[i-1, j], result[i, j-w[i]] + v[i])

3. 解决

a. 分治

public int solution(int[] w, int[] v, int c) {
    return cal(w, v, w.length, c);
}

/** 
 * 当背包容量为j时，第i件物品的决策
 */
public int cal(int[] w, int[] v, int i, int j) {
    // 首先定义返回时机
    if (i < 0 || j <= 0 ) {
        return 0;
    }
    int result = 0;
    if (w[i] > j) {
        result = cal(w, v, i - 1, j);
    } else {
        result = Math.max(cal(w, v, i - 1, j), cal(w, v, i - 1, j - w[i]) + v[i]);
    }
}

b. 动态规划

递归

public int solution(int[] w, int[] v, int c) {
    // 初始化：r = 0 / (必须恰好装满) r[i][0] = 0
    int [][] r = new int [][];
    return cal(w, v, w.length, c, r);
}

/** 
 * 当背包容量为j时，第i件物品的决策
 */
public int cal(int[] w, int[] v, int i, int j, int[][] r) {
    if (i < 0 || j <= 0) {
        return 0;
    }
    // 首先定义返回时机
    if (r[i][j] != null) {
        return r[i][j];
    }
    int result = 0;
    // 装不下，则存储不装该物品的最大值
    if (w[i] > j) {
        result = cal(w, v, i - 1, j);
    } else {
        // 否则，存储装或不装的最大值
        result = Math.max(cal(w, v, i - 1, j), cal(w, v, i - 1, j - w[i]) + v[i]);
    }
    r[i][j] = result;
    return result;
}

迭代

public int solution(int[] w, int[] v, int c) {
    // 初始化：r = 0 / (必须恰好装满) r[i][0] = 0
    int [][] r = new int [][];
    for (int i = 1; i < w.length; i++) {
        for (int j = 0; j < c; j++) {
            if (w[i] > j) {
                r[i][j] = r[i - 1][j];
            } else {
                r[i][j] = Math.max(r[i - 1][j], r[i][j - w[i]] + v[i]);
            }
        }
    }
    return r[w.length][c];
}
空间优化
  • result[j] = max(result[j], result[j - w[i]] + v[i]);

不过此处要注意，需要从后往前遍历。原因是，如果从前往后遍历的话，可能会导致原值被改变，后面再取用的时候，就会导致错误。
例如，当计算 i=3 的时候，r[5] = Math.max(r[5], r[5 - w[3]] + v[3])。当进行后续计算的时候，如果再用到r[5]，那就不再是从 i=2 计算过来的原值了，发生错误。

public int solution(int[] w, int[] v, int c) {
    // 初始化：r = 0 / (必须恰好装满) r[0] = 0
    int[] r = new int[]; 
    for (int i = 0; i < w.length; i++) {
        for (int j = c; j >= w[i]; j--) {
            r[j] = Math.max(r[j], r[j - w[i]] + v[i]);
        }
    }
    return r[r.length - 1];
}

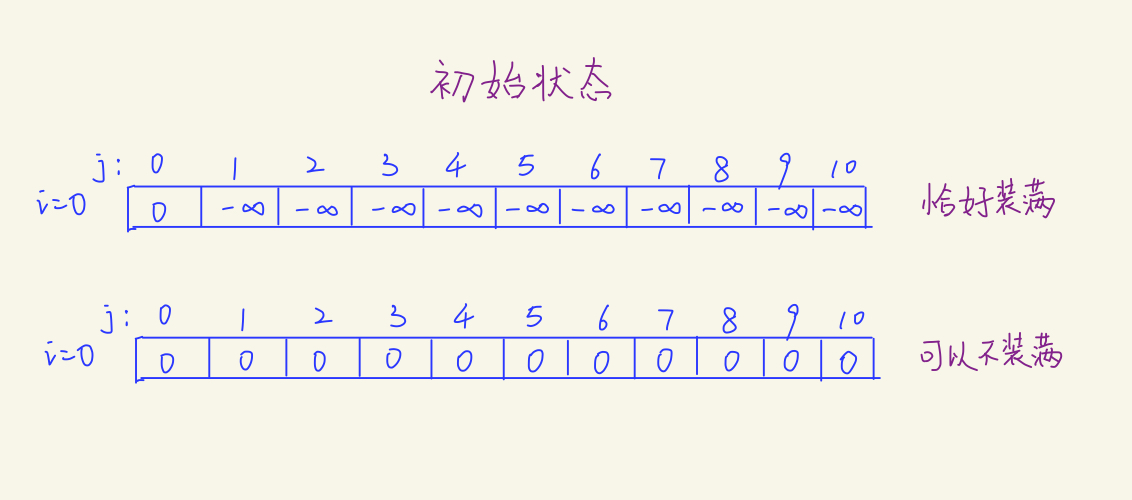
“恰好” 装满

区别在于初始值（对于一维二维都是）。如果需要恰好装满，那么除了j=0以外，初始值应该是负无穷大。如果不需要恰好装满，初始值都为0即可。
因为如果要求恰好装满，那么只有j=0的初始状态是合法的。从别的通道得出的依然会是负无穷大。

原文作者：弗兰克的猫
原文链接：https://www.cnblogs.com/mfrank/p/10533701.html